题目内容
8.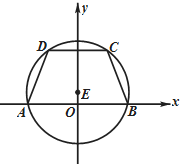 如图所示,等腰梯形ABCD的底边AB在x轴上,顶点A与顶点B关于原点O对称,且底边AB和CD的长分别为6和2$\sqrt{6}$,高为3.
如图所示,等腰梯形ABCD的底边AB在x轴上,顶点A与顶点B关于原点O对称,且底边AB和CD的长分别为6和2$\sqrt{6}$,高为3.(Ⅰ)求等腰梯形ABCD的外接圆E的方程;
(Ⅱ)若点N的坐标为(5,2),点M在圆E上运动,
求线段MN的中点P的轨迹方程.
分析 (Ⅰ)确定四个顶点的坐标,根据对称性判断出E在y轴上,设其坐标,利用两点间的距离公式建立等式求得E的坐标和半径,则圆的方程可得.
(Ⅱ)设出P的坐标,表示出M的坐标代入圆E的方程,进而求得P的轨迹方程.
解答 解:(Ⅰ)由已知可得:A(-3,0),B(3,0),D(-$\sqrt{6}$,3),C($\sqrt{6}$,3),
根据对称性可知,圆心E在y轴上,
设E的坐标为(0,n),
则有9+(n-3)2=6+n2,求得n=2,
∴圆E的圆心为(0,2),半径为$\sqrt{6+4}$=$\sqrt{10}$,
∴圆的方程为:x2+(y-2)2=10.
(Ⅱ)设P坐标为(x,y),
∵P为线段MN的中点,
∴$\frac{5+{x}_{M}}{2}$=x,xM=2x-5,
$\frac{2+{y}_{M}}{2}$=y,yM=2y-2,
代入点M所在圆的方程得:(2x-5)2+(2y-4)2=10,
整理得(x-$\frac{5}{2}$)2+(x-2)2=$\frac{5}{2}$,
∴点P的轨迹方程为(x-$\frac{5}{2}$)2+(x-2)2=$\frac{5}{2}$.
点评 本题主要考查了直线与圆的方程的应用.求圆的方程,一般是确定圆心和半径.解决轨迹方程的问题的步骤先设点,求得变量x和y的关系即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知a>b>0,椭圆C1方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,双曲线C2的方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1,C1与C2离心率之积为$\frac{\sqrt{3}}{2}$,则C2的渐近线方程为( )
| A. | $\sqrt{2}$x±y=0 | B. | x±2y=0 | C. | x±$\sqrt{2}$y=0 | D. | 2x±y=0 |
16.设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为e=$\frac{1}{2}$,右焦点为F(c,0),方程ax2+bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)( )
| A. | 必在圆x2+y2=2上 | B. | 必在圆x2+y2=2外 | ||
| C. | 必在圆x2+y2=2内 | D. | 以上三种情形都有可能 |
 已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的上顶点为A,直线l:y=kx+m交椭圆P,Q两点,设直线AP,AQ的斜率分别为k1,k2.
已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的上顶点为A,直线l:y=kx+m交椭圆P,Q两点,设直线AP,AQ的斜率分别为k1,k2. 如图,设过点N(1,0)的动直线l交椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,且|AB|的最大值为4,椭圆C的离心率e=$\frac{\sqrt{3}}{2}$.
如图,设过点N(1,0)的动直线l交椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,且|AB|的最大值为4,椭圆C的离心率e=$\frac{\sqrt{3}}{2}$.