题目内容
18.已知P是椭圆$\frac{x^2}{100}+\frac{y^2}{36}=1$上的一点,若P到椭圆右准线的距离是$\frac{17}{2}$,则点P到左焦点的距离是$\frac{66}{5}$.分析 利用椭圆的第二定义,可求P到右焦点的距离,然后再根据椭圆的第一定义求出它到左焦点的距离.
解答 解:设F1、F2分别为椭圆的左、右焦点,
P到右准线的距离为d2=$\frac{17}{2}$,
由椭圆的第二定义知,$\frac{|P{F}_{2}|}{{d}_{2}}$=$\frac{c}{a}$=$\frac{8}{10}$,解得|PF2|=$\frac{34}{5}$,
又|PF1|+|PF2|=2a=20,解得|PF1|=$\frac{66}{5}$
故P到它的左焦点的距离为$\frac{66}{5}$.
故答案:$\frac{66}{5}$.
点评 本题主要考查椭圆的基本性质,椭圆的定义的应用,考查计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.公差为正数的等差数列{an}中,a2+a5=12,a3a4=35,则数列{$(\frac{1}{2})^{{a}_{n}}$}的前n项和为( )
| A. | Sn=1-$\frac{1}{{2}^{n}}$ | B. | Sn=$\frac{2}{3}$-$\frac{2}{3•{4}^{n}}$ | C. | Sn=2n+1-2 | D. | Sn=$\frac{{4}^{n+1}-4}{3}$ |
9.M、N分别是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,椭圆上异于M、N于点P满足kPM•kPN=-$\frac{1}{4}$,则椭圆的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{3}$ |
8.函数f(x)=$\frac{{x}^{2}(x+1)}{x+1}$是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
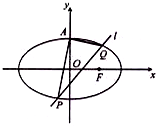 已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的上顶点为A,直线l:y=kx+m交椭圆P,Q两点,设直线AP,AQ的斜率分别为k1,k2.
已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的上顶点为A,直线l:y=kx+m交椭圆P,Q两点,设直线AP,AQ的斜率分别为k1,k2. 在棱锥A-BCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1.
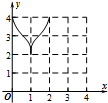
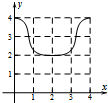
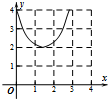
在棱锥A-BCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1.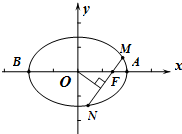 如图:已知方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的椭圆,A,B为顶点,过右焦点的弦MN的长度为y,中心O到弦MN的距离为d,点M从右顶点A开始按逆时针方向在椭圆上移动到B停止,当0°≤∠MFA≤90°时,记x=d,当90°<∠MFA≤180°,记x=2$\sqrt{2}$-d,函数y=f(x)图象是( )
如图:已知方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的椭圆,A,B为顶点,过右焦点的弦MN的长度为y,中心O到弦MN的距离为d,点M从右顶点A开始按逆时针方向在椭圆上移动到B停止,当0°≤∠MFA≤90°时,记x=d,当90°<∠MFA≤180°,记x=2$\sqrt{2}$-d,函数y=f(x)图象是( )