题目内容
1．已知圆C的圆心为坐标原点O，且与直线l1：x-y-2$\sqrt{2}$=0相切．（1）求圆C的方程；
（2）若与直线l1垂直的直线l2与圆C交于不同的两点P、Q，且以PQ为直径的圆过原点，求直线l2的方程．
分析 （1）根据点到直线的距离确定圆的半径，则圆的方程可得．
（2）设出直线l2的方程，判断出△OPQ为等腰直角三角形，求得圆心到直线l2的距离进而利用点到直线的距离求得c．则直线方程可得．
解答 解：（1）由已知圆心到直线的距离为半径，求得半径r=$\frac{2\sqrt{2}}{\sqrt{1+1}}$=2，
∴圆的方程为x2+y2=4．
（2）设直线l2的方程为x+y+c=0，
由已知△OPQ为等腰直角三角形，则圆心到直线l2的距离为1，利用点到直线的距离公式得$\frac{|c|}{\sqrt{2}}$=$\sqrt{2}$，
求得c=±2．
所以直线l2的方程为x+y+2=0或x+y-2=0．
点评 本题主要考查了直线与圆的方程问题的应用．点到直线的距离公式是解决此类问题的常用公式，应灵活运用．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
9．M、N分别是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点，椭圆上异于M、N于点P满足kPM•kPN=-$\frac{1}{4}$，则椭圆的离心率为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{1}{3}$ |
16．设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为e=$\frac{1}{2}$，右焦点为F（c，0），方程ax2+bx-c=0的两个实根分别为x1和x2，则点P（x1，x2）（ ）
| A． | 必在圆x2+y2=2上 | B． | 必在圆x2+y2=2外 | ||
| C． | 必在圆x2+y2=2内 | D． | 以上三种情形都有可能 |
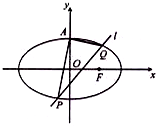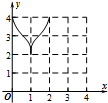
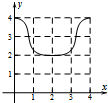
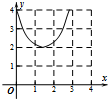
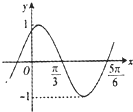
已知椭圆C：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的上顶点为A，直线l：y=kx+m交椭圆P，Q两点，设直线AP，AQ的斜率分别为k1，k2．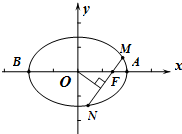
如图：已知方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的椭圆，A，B为顶点，过右焦点的弦MN的长度为y，中心O到弦MN的距离为d，点M从右顶点A开始按逆时针方向在椭圆上移动到B停止，当0°≤∠MFA≤90°时，记x=d，当90°＜∠MFA≤180°，记x=2$\sqrt{2}$-d，函数y=f（x）图象是（ ）
