题目内容

4．若焦点在y轴上的椭圆$\frac{{x}^{2}}{a}$+$\frac{{y}^{2}}{4}$=1的长轴长是短轴的2倍，则a=1．

分析 由题意与椭圆方程得到椭圆的长半轴长和短半轴长，再由长轴长是短轴的2倍列式求得a的值．

解答 解：∵椭圆$\frac{{x}^{2}}{a}$+$\frac{{y}^{2}}{4}$=1的焦点在y轴上，∴4＞a＞0，
且椭圆的长半轴长为2，短半轴长为$\sqrt{a}$，
由长轴长是短轴的2倍，得2=$2\sqrt{a}$，即a=1．
故答案为：1．

点评 本题考查了椭圆的标准方程，考查了椭圆的几何性质，是基础题．

练习册系列答案
相关题目
16．若复数$\frac{5}{2+i}$+ai（a∈R）的模为2，则a的值为（　　）
A．1B．2C．-1D．不存在
17．在数列{an}的前n项和为Sn，2（Sn+1）=3an（n∈N*）．
（1）求数列{an}的通项公式；
（2）设数列{$\frac{2n}{{a}_{n}}$}前n项和为Tn，求证：Tn＜$\frac{9}{4}$．
12．已知椭圆C；$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左右顶点为A，B，点P为椭圆C上不同于A，B，的一点，且直线PA，PB的斜率之积为-$\frac{1}{2}$
（1）求椭圆的离心率；
（2）设F为椭圆C的左焦点，直线l过点F与椭圆C交与不同的两点M，N，且$\overrightarrow{MF}$=3$\overrightarrow{FN}$，求直线l的斜率．
19．已知a＞b＞0，椭圆C1方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1，双曲线C2的方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1，C1与C2离心率之积为$\frac{\sqrt{3}}{2}$，则C2的渐近线方程为（　　）
A．$\sqrt{2}$x±y=0B．x±2y=0C．x±$\sqrt{2}$y=0D．2x±y=0
9．M、N分别是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点，椭圆上异于M、N于点P满足kPM•kPN=-$\frac{1}{4}$，则椭圆的离心率为（　　）
A．$\frac{{\sqrt{2}}}{2}$B．$\frac{{\sqrt{3}}}{3}$C．$\frac{{\sqrt{3}}}{2}$D．$\frac{1}{3}$
16．设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为e=$\frac{1}{2}$，右焦点为F（c，0），方程ax2+bx-c=0的两个实根分别为x1和x2，则点P（x1，x2）（　　）
A．必在圆x2+y2=2上B．必在圆x2+y2=2外
C．必在圆x2+y2=2内D．以上三种情形都有可能
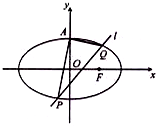13．已知椭圆C：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的上顶点为A，直线l：y=kx+m交椭圆P，Q两点，设直线AP，AQ的斜率分别为k1，k2．
（1）若m=0，时求k1•k2的值；
（2）若k1•k2=-1时，证明直线l：y=kx+m过定点．
14．椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，C、D分别是椭圆的左右顶点，过椭圆右焦点F作弦AB（A，B，C，D不重合）．当直线AB与x轴垂直，|AB|=$\sqrt{2}$．
（Ⅰ）求椭圆的方程；
（Ⅱ）当△OAB的面积为$\frac{2}{3}$时，求直线AB的方程；
（Ⅲ）设直线AC、AD、BC、BD的斜率分别为k1，k2，k3，k4，证明：k1•k2•k3•k4为定值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网