题目内容
已知椭圆的中心为坐标原点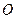 ,焦点在
,焦点在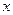 轴上,斜率为
轴上,斜率为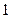 且过椭圆右焦点
且过椭圆右焦点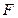 的直线交椭圆于
的直线交椭圆于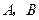 两点,
两点,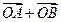 与
与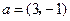 共线.求椭圆的离心率;
共线.求椭圆的离心率;
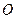 ,焦点在
,焦点在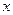 轴上,斜率为
轴上,斜率为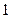 且过椭圆右焦点
且过椭圆右焦点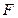 的直线交椭圆于
的直线交椭圆于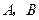 两点,
两点,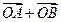 与
与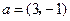 共线.求椭圆的离心率;
共线.求椭圆的离心率;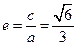
设椭圆方程为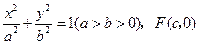 ,
,
则直线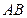 的方程为
的方程为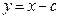 ,代入
,代入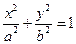 ,
,
化简得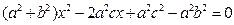 .
.
令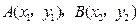 ,则
,则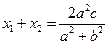 ,
,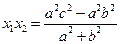 .
.
由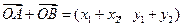 ,
,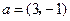 ,
,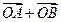 与
与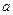 共线,
共线,
得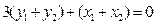 .
.
又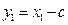 ,
,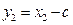 ,
,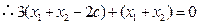 ,
,
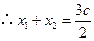 ,即
,即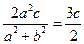 ,所以
,所以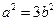 .
.
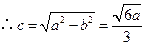 ,故离心率
,故离心率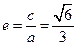 .
.
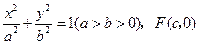 ,
,则直线
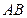 的方程为
的方程为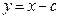 ,代入
,代入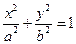 ,
,化简得
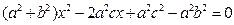 .
.令
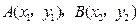 ,则
,则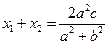 ,
,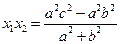 .
.由
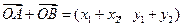 ,
,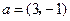 ,
,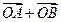 与
与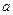 共线,
共线,得
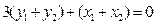 .
.又
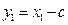 ,
,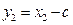 ,
,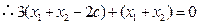 ,
,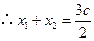 ,即
,即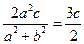 ,所以
,所以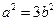 .
.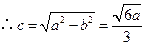 ,故离心率
,故离心率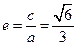 .
.
练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
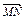 ||
||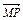 |+
|+ 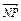 =0,求动点P(x,y)的轨迹方程.
=0,求动点P(x,y)的轨迹方程.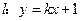 与双曲线
与双曲线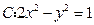 的右支交于不同的两点
的右支交于不同的两点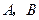 .
.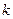 的取值范围;
的取值范围;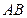 为直径的圆经过双曲线
为直径的圆经过双曲线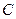 的右焦点
的右焦点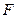 ?若存在,求出
?若存在,求出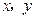 满足
满足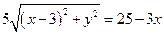 ,求
,求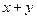 的最大值与最小值.
的最大值与最小值.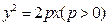 上点
上点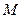 到定点
到定点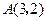 和焦点
和焦点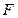 的距离之和的最小值为
的距离之和的最小值为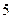 ,求此抛物线的方程.
,求此抛物线的方程.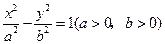 ,
,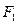 ,
,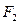 为双曲线的两个焦点,点
为双曲线的两个焦点,点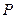 在双曲线上,求
在双曲线上,求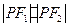 的最小值.
的最小值.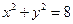 ,定点
,定点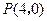 ,问过
,问过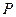 点的直线的斜角在什么范围内取值时,这条直线与圆:(1)相切,(2)相交,(3)相离,并写出过
点的直线的斜角在什么范围内取值时,这条直线与圆:(1)相切,(2)相交,(3)相离,并写出过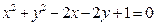 ,点
,点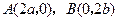 且
且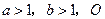 为坐标原点.
为坐标原点.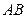 相切时,求
相切时,求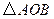 面积最小,求直线
面积最小,求直线 , BC=
, BC=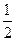 ,椭圆E以A,B为焦点且经过点D. (1)建立适当的直角坐标系,求椭圆E的方程; (2)若点Q满足:
,椭圆E以A,B为焦点且经过点D. (1)建立适当的直角坐标系,求椭圆E的方程; (2)若点Q满足: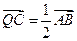 ,问是否存在不平行AB,的直线
,问是否存在不平行AB,的直线 与椭圆E交于M、N两点.且|MQ|=|NQ|.若存在,求直线
与椭圆E交于M、N两点.且|MQ|=|NQ|.若存在,求直线 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.