题目内容
已知两点M(-2,0)、N(2,0),点P为坐标平面内的动点,满足|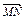 ||
||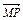 |+
|+ 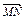 ·
·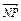 =0,求动点P(x,y)的轨迹方程.
=0,求动点P(x,y)的轨迹方程.
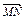 ||
||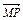 |+
|+ 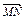 ·
·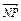 =0,求动点P(x,y)的轨迹方程.
=0,求动点P(x,y)的轨迹方程.y2=-8x
由题意: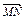 =(4,0),
=(4,0),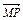 =(x+2,y),
=(x+2,y),
?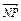 =(x-2,y),
=(x-2,y),
∵|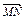 ||
||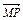 |+
|+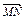 ·
·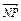 =0,
=0,
∴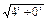 ·
·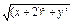 +(x-2)·4+y·0=0,
+(x-2)·4+y·0=0,
两边平方,化简得y2=-8x.
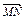 =(4,0),
=(4,0),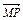 =(x+2,y),
=(x+2,y),?
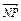 =(x-2,y),
=(x-2,y),∵|
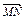 ||
||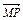 |+
|+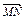 ·
·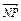 =0,
=0,∴
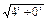 ·
·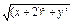 +(x-2)·4+y·0=0,
+(x-2)·4+y·0=0,两边平方,化简得y2=-8x.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
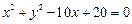 相切,过点P(-4,0)作斜率为
相切,过点P(-4,0)作斜率为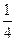 的直线l,使得l和G交于A、B两点,和y轴交于点C,并且点P在线段AB上,又满足
的直线l,使得l和G交于A、B两点,和y轴交于点C,并且点P在线段AB上,又满足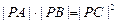
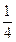 ,则所得曲线的方程是( )
,则所得曲线的方程是( )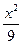 +
+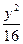 ="1"
="1" 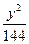 =1
=1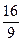 y2="1"
y2="1"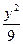 =1
=1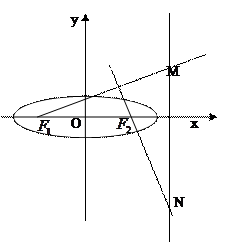 设椭圆
设椭圆 的左右焦点分别为
的左右焦点分别为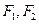 ,离心率
,离心率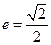 ,过
,过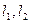 ,且
,且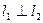 ,
,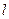 :
: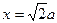 于
于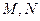 两点。
两点。 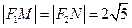 ,求 椭圆的方程;
,求 椭圆的方程;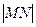 取最小值时,试探究
取最小值时,试探究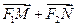 与
与
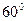 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )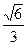
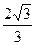
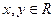 ,
,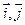 为直角坐标平面内
为直角坐标平面内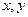 轴正方向上的单位向量,若向量
轴正方向上的单位向量,若向量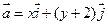 ,
,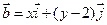 ,且
,且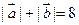 .(1)求点
.(1)求点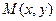 的轨迹
的轨迹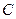 的方程;(2)过点(0,3)作直线
的方程;(2)过点(0,3)作直线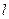 与曲线
与曲线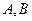 两点,设
两点,设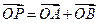 ,是否存在这样的直线
,是否存在这样的直线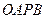 是矩形?若存在,求出直线
是矩形?若存在,求出直线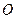 ,焦点在
,焦点在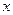 轴上,斜率为
轴上,斜率为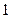 且过椭圆右焦点
且过椭圆右焦点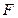 的直线交椭圆于
的直线交椭圆于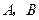 两点,
两点,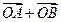 与
与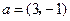 共线.求椭圆的离心率;
共线.求椭圆的离心率;