题目内容
直线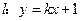 与双曲线
与双曲线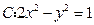 的右支交于不同的两点
的右支交于不同的两点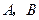 .
.
(1)求实数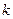 的取值范围;
的取值范围;
(2)是否存在实数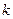 ,使得以线段
,使得以线段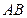 为直径的圆经过双曲线
为直径的圆经过双曲线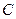 的右焦点
的右焦点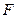 ?若存在,求出
?若存在,求出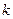 的值,若不存在,说明理由.
的值,若不存在,说明理由.
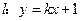 与双曲线
与双曲线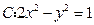 的右支交于不同的两点
的右支交于不同的两点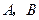 .
.(1)求实数
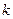 的取值范围;
的取值范围;(2)是否存在实数
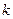 ,使得以线段
,使得以线段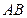 为直径的圆经过双曲线
为直径的圆经过双曲线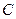 的右焦点
的右焦点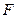 ?若存在,求出
?若存在,求出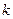 的值,若不存在,说明理由.
的值,若不存在,说明理由.(1) . (2)存在
. (2)存在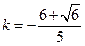
 . (2)存在
. (2)存在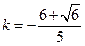
(1)将直线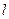 的方程
的方程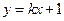 代入双曲线
代入双曲线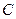 的方程
的方程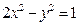 ,
,
整理得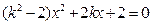 .依题意,直线
.依题意,直线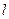 与双曲线
与双曲线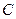 的右支交于不同两点,
的右支交于不同两点,
故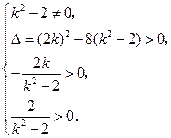 解得
解得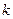 的取值范围为
的取值范围为 .
.
(2)设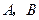 两点的坐标分别为
两点的坐标分别为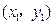 ,
,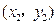 ,
,
则由①式得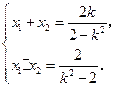 ②
②
假设存在实数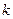 ,使得以线段
,使得以线段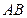 为直径的圆经过双曲线
为直径的圆经过双曲线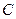 的右焦点
的右焦点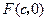 ,
,
则由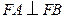 得
得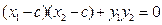 ,
,
即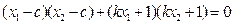 .
.
整理得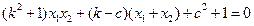 . ③
. ③
把②式及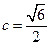 代入③式化简得
代入③式化简得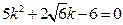 .
.
解得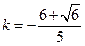 ,或
,或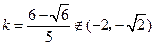 (舍去).
(舍去).
可知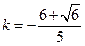 使得以线段
使得以线段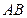 为直径的圆经过双曲线
为直径的圆经过双曲线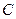 的右焦点.
的右焦点.
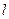 的方程
的方程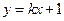 代入双曲线
代入双曲线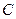 的方程
的方程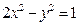 ,
,整理得
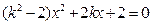 .依题意,直线
.依题意,直线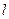 与双曲线
与双曲线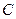 的右支交于不同两点,
的右支交于不同两点,故
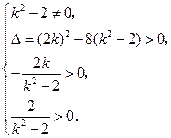 解得
解得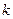 的取值范围为
的取值范围为 .
.(2)设
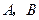 两点的坐标分别为
两点的坐标分别为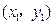 ,
,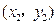 ,
,则由①式得
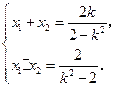 ②
②假设存在实数
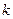 ,使得以线段
,使得以线段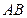 为直径的圆经过双曲线
为直径的圆经过双曲线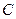 的右焦点
的右焦点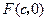 ,
,则由
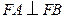 得
得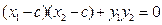 ,
,即
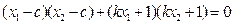 .
.整理得
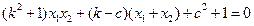 . ③
. ③把②式及
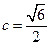 代入③式化简得
代入③式化简得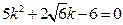 .
.解得
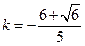 ,或
,或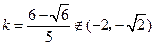 (舍去).
(舍去).可知
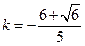 使得以线段
使得以线段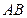 为直径的圆经过双曲线
为直径的圆经过双曲线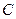 的右焦点.
的右焦点.
练习册系列答案
相关题目
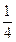 ,则所得曲线的方程是( )
,则所得曲线的方程是( )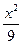 +
+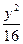 ="1"
="1" 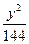 =1
=1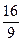 y2="1"
y2="1"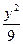 =1
=1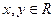 ,
,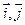 为直角坐标平面内
为直角坐标平面内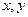 轴正方向上的单位向量,若向量
轴正方向上的单位向量,若向量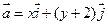 ,
,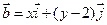 ,且
,且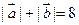 .(1)求点
.(1)求点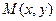 的轨迹
的轨迹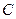 的方程;(2)过点(0,3)作直线
的方程;(2)过点(0,3)作直线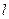 与曲线
与曲线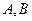 两点,设
两点,设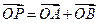 ,是否存在这样的直线
,是否存在这样的直线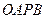 是矩形?若存在,求出直线
是矩形?若存在,求出直线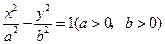 的焦点间的距离,焦点与顶点间的距离,焦点与准线间的距离,准线与准线间的距离,顶点到准线的距离.
的焦点间的距离,焦点与顶点间的距离,焦点与准线间的距离,准线与准线间的距离,顶点到准线的距离. 上求一点
上求一点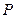 ,使它到左焦点的距离是它到右焦点距离的两倍.
,使它到左焦点的距离是它到右焦点距离的两倍.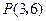 在以两坐标轴为对称轴的椭圆上,你能根据
在以两坐标轴为对称轴的椭圆上,你能根据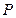 点的坐标最多写出椭圆上几个点的坐标(
点的坐标最多写出椭圆上几个点的坐标(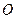 ,焦点在
,焦点在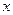 轴上,斜率为
轴上,斜率为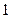 且过椭圆右焦点
且过椭圆右焦点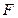 的直线交椭圆于
的直线交椭圆于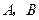 两点,
两点,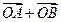 与
与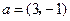 共线.求椭圆的离心率;
共线.求椭圆的离心率;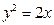 ,过点
,过点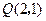 作一直线交抛物线于
作一直线交抛物线于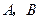 两点,试求弦
两点,试求弦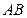 中点的轨迹方程.
中点的轨迹方程.