题目内容
(12分)直角梯形ABCD中, ∠DAB=90°,AD//BC,
AB="2," AD= , BC=
, BC=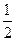 ,椭圆E以A,B为焦点且经过点D. (1)建立适当的直角坐标系,求椭圆E的方程; (2)若点Q满足:
,椭圆E以A,B为焦点且经过点D. (1)建立适当的直角坐标系,求椭圆E的方程; (2)若点Q满足: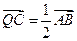 ,问是否存在不平行AB,的直线
,问是否存在不平行AB,的直线 与椭圆E交于M、N两点.且|MQ|=|NQ|.若存在,求直线
与椭圆E交于M、N两点.且|MQ|=|NQ|.若存在,求直线 的斜率
的斜率 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
AB="2," AD=
 , BC=
, BC=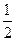 ,椭圆E以A,B为焦点且经过点D. (1)建立适当的直角坐标系,求椭圆E的方程; (2)若点Q满足:
,椭圆E以A,B为焦点且经过点D. (1)建立适当的直角坐标系,求椭圆E的方程; (2)若点Q满足: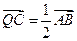 ,问是否存在不平行AB,的直线
,问是否存在不平行AB,的直线 与椭圆E交于M、N两点.且|MQ|=|NQ|.若存在,求直线
与椭圆E交于M、N两点.且|MQ|=|NQ|.若存在,求直线 的斜率
的斜率 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.(1) 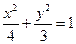 (2)略
(2)略
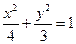 (2)略
(2)略建立如图所示的坐标系
(1)椭圆E的方程为: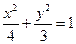 (2)要
(2)要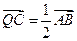 则Q
则Q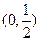 .
.
∵直线 坐标轴,∴设
坐标轴,∴设 方程:
方程: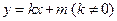 且椭圆相交
且椭圆相交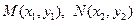 .
.
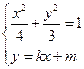 ,
,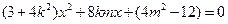
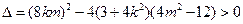 ,即
,即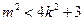 ①
①
又|MQ|=|NQ|,利用中垂线斜率关系:设MN的中点为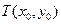
则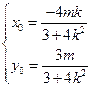 ,∵MN⊥QT ∴
,∵MN⊥QT ∴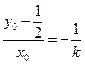 整理:
整理: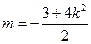
代入到①可知: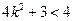 ,∴
,∴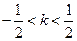 且
且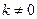 为所求.
为所求.
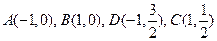
(1)椭圆E的方程为:
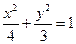 (2)要
(2)要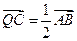 则Q
则Q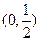 .
.∵直线
 坐标轴,∴设
坐标轴,∴设 方程:
方程: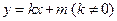 且椭圆相交
且椭圆相交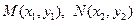 .
.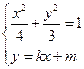 ,
,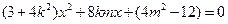
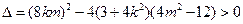 ,即
,即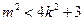 ①
①又|MQ|=|NQ|,利用中垂线斜率关系:设MN的中点为
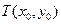
则
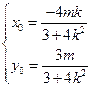 ,∵MN⊥QT ∴
,∵MN⊥QT ∴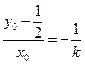 整理:
整理: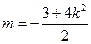
代入到①可知:
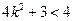 ,∴
,∴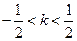 且
且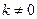 为所求.
为所求.
练习册系列答案
相关题目
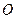 ,焦点在
,焦点在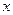 轴上,斜率为
轴上,斜率为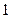 且过椭圆右焦点
且过椭圆右焦点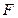 的直线交椭圆于
的直线交椭圆于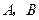 两点,
两点,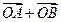 与
与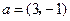 共线.求椭圆的离心率;
共线.求椭圆的离心率;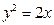 ,过点
,过点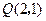 作一直线交抛物线于
作一直线交抛物线于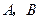 两点,试求弦
两点,试求弦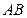 中点的轨迹方程.
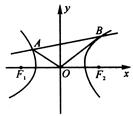
中点的轨迹方程.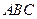 的两个顶点
的两个顶点 的坐标分别为
的坐标分别为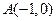 ,
,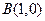 ,平面内两点
,平面内两点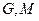 同时满足下列条件:①
同时满足下列条件:①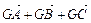 =0;②
=0;②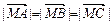 ;③
;③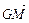 ∥
∥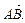 (1)求△
(1)求△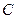 的轨迹方程;(2)过点
的轨迹方程;(2)过点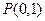 直线
直线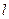 与(1)中轨迹交于不同的两点
与(1)中轨迹交于不同的两点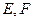 ,求△
,求△ 面积的最大值.
面积的最大值.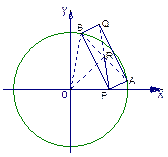
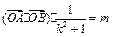 ,且满足2≤m≤4时,
,且满足2≤m≤4时,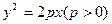
 :
: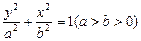 的离心率
的离心率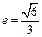 ,过点
,过点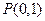 的直线
的直线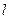 与椭圆
与椭圆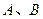 两点,且
两点,且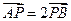 ,求
,求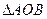 面积的最大值及取得最大值时椭圆的方程.
面积的最大值及取得最大值时椭圆的方程.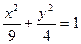
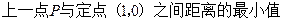 .
.