题目内容
8．已知物体的运动方程是s=t2+$\frac{3}{t}$（t的单位：秒，s的单位：米），则物体在t=4时的速度v=$\frac{126}{16}$m/s．分析 求函数的导数，根据导数的物理意义进行求解即可．
解答 解：函数的导数为s′=2t-$\frac{3}{{t}^{2}}$，
则当t=4时的速度v=s′=2×4-$\frac{3}{{4}^{2}}$=8-$\frac{3}{16}$=$\frac{126}{16}$，
故答案为：$\frac{126}{16}$
点评 本题主要考查导数的计算，根据导数的物理意义是解决本题的关键．比较基础．
练习册系列答案
相关题目
14．某同学在研究性学习中，收集到某制药厂今年2-6月甲胶囊产量（单位：千盒）的数据如下表所示：
若该同学用最小二乘法求得线性回归方程为$\widehat{y}$=1.23x+a，则实数a=0.08．
| 月份 | 2 | 3 | 4 | 5 | 6 |
| y（千盒） | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
3．下表提供了某厂生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据．
（1）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程$\widehaty$=$\hat b$x+$\hat a$；
（2）请求出相关指数R2，并说明残差变量对预报变量的影响约占百分之几．
（参考数值：3×2.5+4×3+5×4+6×4.5=66.5）
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
（2）请求出相关指数R2，并说明残差变量对预报变量的影响约占百分之几．
（参考数值：3×2.5+4×3+5×4+6×4.5=66.5）
20．已知直线l的方程为y=x+1，则它的倾斜角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
18．
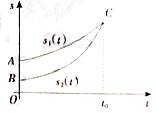甲、乙两人走过的路程s1（t），s2（t）与时间t的关系如图，则在[0，t0]这个时间段内，甲、乙两人的平均速度v甲、v乙的关系是（ ）
甲、乙两人走过的路程s1（t），s2（t）与时间t的关系如图，则在[0，t0]这个时间段内，甲、乙两人的平均速度v甲、v乙的关系是（ ）| A． | v甲＞v乙 | B． | v甲＜v乙 | C． | v甲=v乙 | D． | 大小关系不确定 |