题目内容

18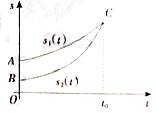．甲、乙两人走过的路程s1（t），s2（t）与时间t的关系如图，则在[0，t0]这个时间段内，甲、乙两人的平均速度v甲、v乙的关系是（　　）
A．v甲＞v乙B．v甲＜v乙C．v甲=v乙D．大小关系不确定

分析 由图象可得s1（t）＜s2（t），且他们用的时间相等，都是t0，则由甲、乙两人的平均速度v甲 =$\frac{{s}_{1}（t）}{{t}_{0}}$，v乙=$\frac{{s}_{2}（t）}{{t}_{0}}$，可得v甲、v乙的关系．

解答 解：由于甲、乙两人走过的路程s1（t），s2（t）满足 s1（t）＜s2（t），且他们用的时间相等，都是t0，
则由甲、乙两人的平均速度v甲 =$\frac{{s}_{1}（t）}{{t}_{0}}$，v乙=$\frac{{s}_{2}（t）}{{t}_{0}}$，可得s1（t）＜s2（t），
故选：B．

点评 本题主要考查函数的图象，平均速度的定义，属于基础题．

练习册系列答案
相关题目
8．已知物体的运动方程是s=t2+$\frac{3}{t}$（t的单位：秒，s的单位：米），则物体在t=4时的速度v=$\frac{126}{16}$m/s．
9．若过A（-2，m）和B（m，4）的直线与斜率为-2的直线平行，则m的值为（　　）
A．-8B．0C．2D．10
6．定义一种运算如下：$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$=ad-bc，则复数$[\begin{array}{l}{1-i}&{-1}\\{2}&{3i}\end{array}]$的共轭复数是5-3i．
13．若不等式（1-x）eax＜1+x在x∈（0，1）上恒成立，则实数a的取值范围为（-∞，2]．
3．如图所示的程序框图，若输出结果是990，则判断框内应填入的条件是（　　）
A．i≥10B．i＜10C．i≥9D．i＜9
10．直线ax+2y-1=0与2x+（a-1）y+1=0垂直，则a=$\frac{1}{2}$．
7．在平面直角坐标系xoy中，A、B、C是圆x2+y2=1上相异三点，若存在正实数λ，μ，使得$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$，则λ2+（μ-3）2的取值范围是（　　）
A．[0，+∞）B．（2，+∞）C．[2，+∞）D．（8，+∞）
8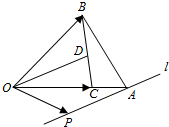．在△OAB中，C为OA上的一点，且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$，D是BC的中点，过点A的直线l∥OD，P是直线l上的动点，若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$，则λ1-λ2=（　　）
A．$\frac{3}{2}$B．-$\frac{3}{2}$C．$\frac{5}{4}$D．-$\frac{5}{4}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网