题目内容
20．已知直线l的方程为y=x+1，则它的倾斜角为（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
分析 由直线方程求出直线的斜率，由k=tanα求出直线的倾斜角．
解答 解：由题意知，直线l的方程为y=x+1，
则直线的斜率k=1，所以直线的倾斜角是$\frac{π}{4}$，
故选：B．
点评 本题考查直线的方程、直线的斜率和倾斜角之间的关系，属于基础题．
练习册系列答案
相关题目
5．
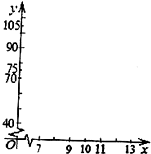下表是随机抽取的某市五个地段五种不同户型新电梯房面积x（单位：十平方米）和相应的房价y（单位：万元）统计表：
（Ⅰ）在给定的坐标系中画出散点图；
（Ⅱ）求用最小二乘法得到的回归直线方程（参考公式和数据：$\widehat{y}$=$\frac{\underset{\stackrel{n}{∑}}{i=1}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\underset{\stackrel{n}{∑}}{i=1}{x}_{i}^{2}-n•{\overline{x}}^{2}}$，$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，$\underset{\stackrel{5}{∑}}{i=1}$xiyi=4010）；
（Ⅲ）请估计该市一面积为120m2的新电梯房的房价．
下表是随机抽取的某市五个地段五种不同户型新电梯房面积x（单位：十平方米）和相应的房价y（单位：万元）统计表：| x | 7 | 9 | 10 | 11 | 13 |
| y | 40 | 75 | 70 | 90 | 105 |
（Ⅱ）求用最小二乘法得到的回归直线方程（参考公式和数据：$\widehat{y}$=$\frac{\underset{\stackrel{n}{∑}}{i=1}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\underset{\stackrel{n}{∑}}{i=1}{x}_{i}^{2}-n•{\overline{x}}^{2}}$，$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，$\underset{\stackrel{5}{∑}}{i=1}$xiyi=4010）；
（Ⅲ）请估计该市一面积为120m2的新电梯房的房价．
11．用反证法证明命题“a，b∈N，如果ab可被5整除，那么a，b至少有1个能被5整除．则假设的内容是（ ）
| A． | a，b都能被5整除 | B． | a，b有1个不能被5整除 | ||
| C． | a不能被5整除 | D． | a，b都不能被5整除 |
15．下列向量的运算中，正确的是（ ）
| A． | $\overrightarrow{AB}+\overrightarrow{BA}=2\overrightarrow{AB}$ | B． | $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{CA}$ | C． | $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$ | D． | $\overrightarrow{AB}-\overrightarrow{AD}-\overrightarrow{DC}=\overrightarrow{BC}$ |
5．y=x-ln（1+x）的单调递增区间是（ ）
| A． | （-1，0 ） | B． | （-1，+∞） | C． | （0，+∞） | D． | （1，+∞） |
12．在数列{an}中，如果存在非零常数T，使得am+T=am对于任意的非零自然数 均成立，那么就称数列{an}为周期数列，其中T 叫数列{an}的周期．已知数列{xn}满足xn+1=|xn-xn-1|（n≥2），如果x1=1，x2=a（a∈R，a≠0），当数列{xn}的周期最小时，该数列前2012项的和是（ ）
| A． | 670 | B． | 671 | C． | 1341 | D． | 1342 |
9．若过A（-2，m）和B（m，4）的直线与斜率为-2的直线平行，则m的值为（ ）
| A． | -8 | B． | 0 | C． | 2 | D． | 10 |