题目内容
【题目】已知函数![]() (
(![]() ,
,![]() ).
).
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() ,求k的取值范围.
,求k的取值范围.
【答案】(1)详见解析(2)![]() 或
或![]()
【解析】
(1)将函数求导并化简,对![]() 分成
分成![]() 两种情况,讨论函数
两种情况,讨论函数![]() 的单调性.(2)原不等式即
的单调性.(2)原不等式即![]() (
(![]() ),当
),当![]() 时,上述不等式显然成立.当
时,上述不等式显然成立.当![]() 时,将不等式变为
时,将不等式变为![]() ,构造函数
,构造函数![]() ,利用导数研究函数的单调性,由此求得
,利用导数研究函数的单调性,由此求得![]() 的取值范围.
的取值范围.
解:(1)![]()
![]()
![]() .
.
①若![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
②若![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
∴当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)![]() (
(![]() ),
),
当![]() 时,上不等式成立,满足题设条件;
时,上不等式成立,满足题设条件;
当![]() 时,
时,![]() ,等价于
,等价于![]() ,
,
设![]() ,则
,则![]()
![]() ,
,
设![]() (
(![]() ),则
),则![]() ,
,
∴![]() 在
在![]() 上单调递减,得
上单调递减,得![]() .
.
①当![]() ,即
,即![]() 时,得
时,得![]() ,
,![]() ,
,
∴![]() 在
在![]() 上单调递减,得
上单调递减,得![]() ,满足题设条件;
,满足题设条件;
②当![]() ,即
,即![]() 时,
时,![]() ,而
,而![]() ,
,
∴![]() ,
,![]() ,又
,又![]() 单调递减,
单调递减,
∴当![]() ,
,![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上单调递增,得
上单调递增,得![]() ,不满足题设条件;
,不满足题设条件;
综上所述,![]() 或
或![]() .
.

 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】2019年9月23日,在![]() 省
省![]() 市举办的2019年中国农民丰收节“新电商与农业科技创新”论坛上,来自政府相关部门的领导及11所中国高校的专家学者以“农业科技创新与乡村振兴”、“新农人与脱贫攻坚”为核心议题各抒己见,农产品方面的科技创新越来越成为21世纪大国崛起的一项重大突破.科学家对某农产品每日平均增重量
市举办的2019年中国农民丰收节“新电商与农业科技创新”论坛上,来自政府相关部门的领导及11所中国高校的专家学者以“农业科技创新与乡村振兴”、“新农人与脱贫攻坚”为核心议题各抒己见,农产品方面的科技创新越来越成为21世纪大国崛起的一项重大突破.科学家对某农产品每日平均增重量![]() (单位:
(单位:![]() )与每日营养液注射量
)与每日营养液注射量![]() (单位:
(单位:![]() )之间的关系统计出表1一组数据:
)之间的关系统计出表1一组数据:
表1
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3.5 | 5 | 6.6 | 8.4 |
(1)根据表1和表2的相关统计值求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)计算拟合指数![]() 的值,并说明线性回归模型的拟合效果(
的值,并说明线性回归模型的拟合效果(![]() 的值在.98以上说明拟合程度好);
的值在.98以上说明拟合程度好);
(3)若某日该农产品的营养液注释量为![]() ,预测该日这种农产品的平均增长重量(结果精确到0.1).
,预测该日这种农产品的平均增长重量(结果精确到0.1).
附:①
表2
|
|
|
|
92.4 | 55 | 25 | 0.04 |
②对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: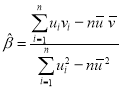 ,
,![]() ,
,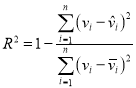 .
.