题目内容
13．如图，已知AB是半径为5的圆O的弦，过点A，B的切线交于点P，若AB=6，则PA等于（ ）
| A． | $\frac{5}{2}\sqrt{21}$ | B． | $\frac{25}{4}$ | C． | $\frac{15}{4}$ | D． | $\frac{3}{2}\sqrt{5}$ |
分析 连接OP，交AB于C，求出OC，OP，利用勾股定理求出PA．
解答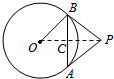 
解：连接OP，交AB于C，则
∵过点A，B的切线交于点P，
∴OB⊥BP，OP⊥AB，
∵AB=6，OB=5，
∴OC=4，
∵OB2=OC•OP，
∴25=4OP，
∴OP=$\frac{25}{4}$，
∴CP=$\frac{9}{4}$，
∴PA=$\sqrt{9+\frac{81}{16}}$=$\frac{15}{4}$，
故选：C．
点评 本题考查圆的切线的性质，考查勾股定理，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
3．在△ABC中，∠A=120°，AC=$\sqrt{3}$，AB=2$\sqrt{3}$，O为BC的中点，则AO=（ ）
| A． | $\sqrt{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{9}{4}$ | D． | 9 |
1．在△ABC中，内角A、B、C的对边分别是a，b，c，a=$\sqrt{2}$，b=$\sqrt{3}$，B=60°，则A=（ ）
| A． | 45° | B． | 60° | C． | 120°或60° | D． | 135°或45° |
