题目内容
20.如图1,在梯形ABCE中,AB∥CE,D是CE的中点,BC∥AD,AB=BC=2,∠BAD=60°,沿AD把梯形折成如图2所示的四棱锥E-ABCD.(1)求证:AD⊥EB;
(2)当平面EAD⊥平面ABCD时,求四棱锥E-ABCD的体积.

分析 (1)首先根据题中的已知条件求出相关的线段长,然后根据所求的结果来进一步判断线面垂直,最后转化为线线垂直.
(2)取AD的中点F,则EF⊥平面ABCD,再求四棱锥E-ABCD的体积.
解答  (1)证明:梯形ABCE中,AB∥CE,D是CE中点,BC∥AD,AB=BC=2,∠BAD=60°连结BE交AD于M点,
(1)证明:梯形ABCE中,AB∥CE,D是CE中点,BC∥AD,AB=BC=2,∠BAD=60°连结BE交AD于M点,
在△ABE中利用余弦定理:BE2=AE2+AB2-2AE•ABcos∠EAB,
解得:BE=2√3且△ABE为等边三角形,EM=EB=√3,
AD⊥EM,
根据梯形的边角关系求得:AD⊥BM,
∴AD⊥面EMB,
∴BE?面EMB,
∴AD⊥BE;
(2)解:取AD的中点F,则EF⊥AD,
∵EF⊥AD,平面EAD⊥平面ABCD,平面EAD⊥平面ABCD=AD,
∴EF⊥平面ABCD,
∵EF=√3,SABCD=AB•ADsin60°=2×2×√32=2√3,
∴VE-ABCD=13×2√3×√3=2.
点评 本题考查的勾股定理及余弦定理,线面垂直的判定及性质定理,考查四棱锥E-ABCD的体积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.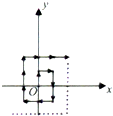 如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )
如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )
 如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )
如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )| A. | (-21,12) | B. | (-22,12) | C. | (-21,13) | D. | (-22,13) |
13.如图,已知AB是半径为5的圆O的弦,过点A,B的切线交于点P,若AB=6,则PA等于( )


| A. | 52√21 | B. | 254 | C. | 154 | D. | 32√5 |
8.若sin(π5+θ)=45,则cos(2π5+2θ)=( )
| A. | 725 | B. | −725 | C. | 2425 | D. | −2425 |
9.设函数f(x)=\left\{{\begin{array}{l}{{x^3}(0≤x<5)}\\{f(x-5)(x≥5)}\end{array}},那么f(2015)=( )
| A. | 27 | B. | 9 | C. | 0 | D. | 1 |
10.以下各式中错误的是( )
| A. | arcsin1=π2 | B. | arccos(-1)=π | C. | arctan0=0 | D. | arccos1=2π |