题目内容
4.(1)求函数f(x)=$\frac{lnx}{x}$的单调区间;(2)设An=nn+1,Bn=(n+1)n(n∈N*).
①实验:分别就n=1,2,3,4,比较An与Bn的大小;
②根据①的实验结果猜测一个一般性结论,并证明你的结论.
分析 (1)先求出函数的导数,解关于导函数的不等式,从而求出函数的单调区间;
(2)①n分别取1,2,3,4,从而比较出大小;②由①猜想:当n≥3且n∈N+时,An>Bn,分别采用函数的单调性或数学归纳法证明即可.
解答 解:(1)f′(x)=$\frac{1-lnx}{{x}^{2}}$,x>0,
当0<x<e时,f′(x)>0,当x>e时,f′(x)<0,
∴f(x)在(0,e)递减,在(e,+∞)递增;
(2)①当n=1时,A1=1,B1=2,A1<B1,
当n=2时,A2=8,B2=9,A2<B2,
当n=3时,A3=81,B3=64,A3>B3,
当n=4时,A4=1024,B4=625,A4>B4,
②由①猜想:当n≥3且n∈N+时,An>Bn,
证明如下:
方法(一):由(1)f(x)在区间(e,+∞)单调递减,
n≥3时,f(n+1)<f(n),即$\frac{ln(n+1)}{n+1}$<$\frac{lnn}{n}$,
∴nln(n+1)<(n+1)lnn,
∴ln(n+1)n<lnnn+1,
∴(n+1)n<nn+1,即Bn<An,
∴当n≥3且n∈N+时,An>Bn,
方法(二):用数学归纳法证明:
1°:当n=3时成立,
2°:设n=k(k≥3,k∈N+)时,猜想成立,即有kk+1>(k+1)k①,
则n=k+1时,由①得:$\frac{{k}^{k+1}}{{(k+1)}^{k}}$>1,
又(k+1)2>k(k+2),即$\frac{k+1}{k+2}$>$\frac{k}{k+1}$,
∴$\frac{{(k+1)}^{k+2}}{{(k+2)}^{k+1}}$=${(\frac{k+1}{k+2})}^{k}$•$\frac{{(k+1)}^{2}}{k+2}$>${(\frac{k}{k+1})}^{k}$•$\frac{k(k+2)}{k+2}$=$\frac{{k}^{k+1}}{{(k+1)}^{k}}$>1,
∴(k+1)k+2>(k+2)k+1,即An+1>Bn+1,
∴n=k+1成立,
∴综合1°,2°当n≥3且n∈N+时,An>Bn.
点评 本题考查了函数的单调性问题,考查导数的应用,不等式的证明,是一道中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 圆 | B. | 抛物线 | C. | 椭圆 | D. | 双曲线 |
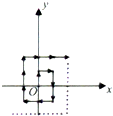 如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )
如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )| A. | (-21,12) | B. | (-22,12) | C. | (-21,13) | D. | (-22,13) |

| A. | $\frac{5}{2}\sqrt{21}$ | B. | $\frac{25}{4}$ | C. | $\frac{15}{4}$ | D. | $\frac{3}{2}\sqrt{5}$ |