题目内容
1.(1)求直线$ρ=\frac{1}{acosθ+bsinθ}$与圆ρ=2ccosθ(c>0)相切的条件;(2)求曲线θ=0,$θ=\frac{π}{3}({ρ≥0})$和ρ=4所围成图形的面积.
分析 (1)直线$ρ=\frac{1}{acosθ+bsinθ}$,化为ax+by=1,圆ρ=2ccosθ(c>0)化为ρ2=2cρcosθ,利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$可得直角坐标方程.利用直线与圆相切的充要条件、点到直线的距离公式即可得出.
(2)曲线θ=0,$θ=\frac{π}{3}({ρ≥0})$和ρ=4所围成图形是如图所示的扇形.利用扇形的面积计算公式即可得出.
解答 解:(1)直线$ρ=\frac{1}{acosθ+bsinθ}$,化为ax+by=1,圆ρ=2ccosθ(c>0)化为ρ2=2cρcosθ,
化为x2+y2=2cx,配方为:(x-c)2+y2=c2.可得圆心(c,0),半径r=c.
∵直线与圆相切,
∴$\frac{|ac-1|}{\sqrt{{a}^{2}+{b}^{2}}}$=c,化为b2c2+2ac=1.
(2)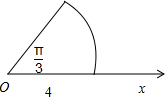 曲线θ=0,$θ=\frac{π}{3}({ρ≥0})$和ρ=4所围成图形是如图所示的扇形.
曲线θ=0,$θ=\frac{π}{3}({ρ≥0})$和ρ=4所围成图形是如图所示的扇形.
∴$S=\frac{1}{2}×{4}^{2}×\frac{π}{3}$=$\frac{8π}{3}$.
点评 本题考查了圆的极坐标方程、直线的极坐标方程、直线与圆相切的充要条件、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.如图,已知AB是半径为5的圆O的弦,过点A,B的切线交于点P,若AB=6,则PA等于( )


| A. | $\frac{5}{2}\sqrt{21}$ | B. | $\frac{25}{4}$ | C. | $\frac{15}{4}$ | D. | $\frac{3}{2}\sqrt{5}$ |
9.设函数f(x)=$\left\{{\begin{array}{l}{{x^3}(0≤x<5)}\\{f(x-5)(x≥5)}\end{array}}$,那么f(2015)=( )
| A. | 27 | B. | 9 | C. | 0 | D. | 1 |
16.设直线l1、l2的方向向量分别为$\overrightarrow a$=(2,-2,-2),$\overrightarrow b$=(2,0,4),则直线l1、l2的夹角余弦值是( )
| A. | $\frac{\sqrt{15}}{15}$ | B. | -$\frac{\sqrt{210}}{15}$ | C. | $\frac{\sqrt{210}}{15}$ | D. | -$\frac{\sqrt{15}}{15}$ |
13.在△ABC中,角A,B,C成单调递增的等差数列,a,b,c是的△ABC三边,$b=\frac{{\sqrt{3}}}{2}$,则c-a的取值范围是( )
| A. | $(0,\frac{1}{4})$ | B. | $(0,\frac{{\sqrt{3}}}{2})$ | C. | $(0,\frac{1}{2})$ | D. | ($\frac{1}{4}$,$\frac{\sqrt{3}}{2}$) |
10.以下各式中错误的是( )
| A. | arcsin1=$\frac{π}{2}$ | B. | arccos(-1)=π | C. | arctan0=0 | D. | arccos1=2π |
11.函数f(x)=$\frac{1}{2}$x2-ln x的最小值( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 不存在 | D. | 0 |