题目内容
8.若n∈N*,且3C${\;}_{n-1}^{n-5}$=5A${\;}_{n-2}^{2}$,则n的值为( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
分析 根据组合数与排列数的公式,列出方程,求出n的值即可.
解答 解:∵n∈N*,且3C${\;}_{n-1}^{n-5}$=5A${\;}_{n-2}^{2}$,
∴3•$\frac{(n-1)(n-2)(n-3)(n-4)}{4×3×2×1}$=5×(n-2)(n-3),
即(n-1)(n-4)=40,
化简得n2-5n-36=0;
解得n=9或n=-4(不合题意,舍去),
∴n的值为9.
故选:B.
点评 本题考查了组合数与排列数公式的应用问题,是基础题目.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
13.如图,已知AB是半径为5的圆O的弦,过点A,B的切线交于点P,若AB=6,则PA等于( )


| A. | $\frac{5}{2}\sqrt{21}$ | B. | $\frac{25}{4}$ | C. | $\frac{15}{4}$ | D. | $\frac{3}{2}\sqrt{5}$ |
16.设直线l1、l2的方向向量分别为$\overrightarrow a$=(2,-2,-2),$\overrightarrow b$=(2,0,4),则直线l1、l2的夹角余弦值是( )
| A. | $\frac{\sqrt{15}}{15}$ | B. | -$\frac{\sqrt{210}}{15}$ | C. | $\frac{\sqrt{210}}{15}$ | D. | -$\frac{\sqrt{15}}{15}$ |
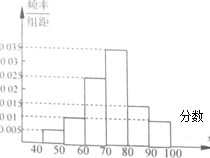 对100名学生的学习成绩进行统计,得到样本频率直方图如图所示,现规定不低于70分为合格,则合格的人数是60.
对100名学生的学习成绩进行统计,得到样本频率直方图如图所示,现规定不低于70分为合格,则合格的人数是60.