题目内容
1．在△ABC中，内角A、B、C的对边分别是a，b，c，a=$\sqrt{2}$，b=$\sqrt{3}$，B=60°，则A=（ ）| A． | 45° | B． | 60° | C． | 120°或60° | D． | 135°或45° |
分析 根据正弦定理进行求解即可．
解答 解：∵a=$\sqrt{2}$，b=$\sqrt{3}$，B=60°，
∴a＜b，则A＜B，
∵$\frac{a}{sinA}=\frac{b}{sinB}$得sinA=$\frac{asinB}{b}=\frac{\sqrt{2}×\frac{\sqrt{3}}{2}}{\sqrt{3}}$=$\frac{\sqrt{2}}{2}$，
∴A=45°，
故选：A
点评 本题主要考查解三角形的应用，利用正弦定理是解决本题的关键．比较基础．
练习册系列答案
相关题目
12．
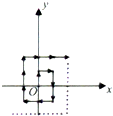如图所示，质点A从坐标原点O开始沿箭头所指方向作规则运动，每次只运动一个单位，相应的质点的坐标记为An，如A1（0，1），A2（1，1），A3（1，0），A4（1，-1），…，则A2015的坐标为（ ）
如图所示，质点A从坐标原点O开始沿箭头所指方向作规则运动，每次只运动一个单位，相应的质点的坐标记为An，如A1（0，1），A2（1，1），A3（1，0），A4（1，-1），…，则A2015的坐标为（ ）| A． | （-21，12） | B． | （-22，12） | C． | （-21，13） | D． | （-22，13） |
13．如图，已知AB是半径为5的圆O的弦，过点A，B的切线交于点P，若AB=6，则PA等于（ ）
| A． | $\frac{5}{2}\sqrt{21}$ | B． | $\frac{25}{4}$ | C． | $\frac{15}{4}$ | D． | $\frac{3}{2}\sqrt{5}$ |
8．若sin（$\frac{π}{5}$+θ）=$\frac{4}{5}$，则cos（$\frac{2π}{5}$+2θ）=（ ）
| A． | $\frac{7}{25}$ | B． | $-\frac{7}{25}$ | C． | $\frac{24}{25}$ | D． | $-\frac{24}{25}$ |