题目内容
若函数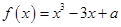 有3个不同的零点,则实数a的取值范围是( )
有3个不同的零点,则实数a的取值范围是( )
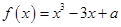 有3个不同的零点,则实数a的取值范围是( )
有3个不同的零点,则实数a的取值范围是( )| A.(-2,2) | B.[-2,2] | C.(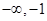 ) ) | D.(1,+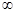 ) ) |
A
解:由函数f(x)=x3-3x+a有三个不同的零点,
则函数f(x)有两个极值点,极小值小于0,极大值大于0;
由f′(x)=3x2-3=3(x+1)(x-1)=0,解得x1=1,x2=-1,
所以函数f(x)的两个极,x∈(-∞,-1),f′(x)>0,x∈(-1,1),f′(x)<0,x∈(1,+∞),f′(x)>0,
∴函数的极小值f(1)=a-2和极大值f(-1)=a+2.
因为函数f(x)=x3-3x+a有三个不同的零点,
所以a+2>0,a-2<0解之,得-2<a<2
故实数a的取值范围是(-2,2).

练习册系列答案
相关题目
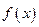 是定义在
是定义在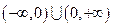 上的函数,且
上的函数,且
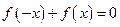 ,当
,当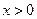 时,
时,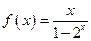 .
.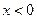 时,
时,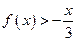
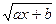 又在其反函数的图象上,求a, b的值
又在其反函数的图象上,求a, b的值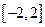 上的奇函数
上的奇函数 满足当
满足当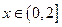 时,
时,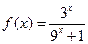 .
.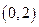 上的单调性,并给予证明;
上的单调性,并给予证明;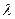 为何值时,关于方程
为何值时,关于方程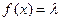 在
在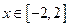 上有实数解?
上有实数解?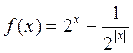
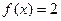 ,求
,求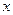 的值;
的值;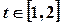 ,
,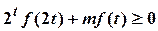 恒成立,求实数
恒成立,求实数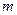 的取值范围。
的取值范围。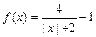 的定义域是
的定义域是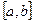 (
(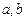 为整数),值域是
为整数),值域是 ,则满
,则满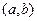 共有_________个
共有_________个