题目内容
已知函数f(x)=x3+mx2+nx-2的图象过点(-1,-6),且函数g(x)=f′(x)+6x是偶函数.
(Ⅰ)求m、n的值;(Ⅱ)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
(Ⅰ)求m、n的值;(Ⅱ)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
解:(Ⅰ)由函数f(x)图象过点(-1,-6),得m-n=-3,①………………1分
由f(x)=x3+mx2+nx-2,得f′(x)=3x2+2mx+n,………………………………………2分
则g(x)=f′(x)+6x=3x2+(6+2m)x+n;
而g(x)图象关于y轴对称,所以-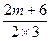 =0,所以m=-3,
=0,所以m=-3,
代入①得n=0.………………………………………………………………………4分
(Ⅱ)由(Ⅰ)得f′(x)=3x(x-2),
令f′(x)=0得x=0或x=2.…………………………………………………………5分
当x变化时,f′(x)、f(x)的变化情况如下表:

由此可得:
当0<a<1时,f(x)在(a-1,a+1)内有极大值f( 0)=-2,无极小值;
0)=-2,无极小值;
当a=1时,f(x)在(a-1,a+1)内无极值;
当1<a<3时,f(x)在(a-1,a+1)内有极小值f(2)=-6,无极大值;
当a≥3时,f(x)在(a-1,a+1)内无极值.…………………………………………11分
综上得:当0<a<1时,f(x)有极大值-2,无极小值,当1<a<3时,有极小值-6,无极大值,当a=1或a≥3时,f(x)无极值.………………………… ………………12分
………………12分
由f(x)=x3+mx2+nx-2,得f′(x)=3x2+2mx+n,………………………………………2分
则g(x)=f′(x)+6x=3x2+(6+2m)x+n;
而g(x)图象关于y轴对称,所以-
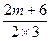 =0,所以m=-3,
=0,所以m=-3,代入①得n=0.………………………………………………………………………4分
(Ⅱ)由(Ⅰ)得f′(x)=3x(x-2),
令f′(x)=0得x=0或x=2.…………………………………………………………5分
当x变化时,f′(x)、f(x)的变化情况如下表:

由此可得:
当0<a<1时,f(x)在(a-1,a+1)内有极大值f(
 0)=-2,无极小值;
0)=-2,无极小值;当a=1时,f(x)在(a-1,a+1)内无极值;
当1<a<3时,f(x)在(a-1,a+1)内有极小值f(2)=-6,无极大值;
当a≥3时,f(x)在(a-1,a+1)内无极值.…………………………………………11分
综上得:当0<a<1时,f(x)有极大值-2,无极小值,当1<a<3时,有极小值-6,无极大值,当a=1或a≥3时,f(x)无极值.…………………………
 ………………12分
………………12分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
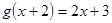 ,则
,则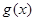 的表达式是( )
的表达式是( )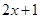 B
B 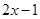 C
C 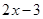 D
D 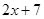
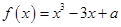 有3个不同的零点,则实数a的取值范围是( )
有3个不同的零点,则实数a的取值范围是( )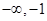 )
)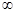 )
)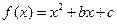 为偶函数,曲线
为偶函数,曲线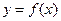 过点
过点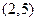 ,
,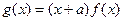 .
.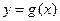 存在斜率为0的切线,求实数
存在斜率为0的切线,求实数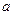 的取值范围;
的取值范围;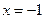 时函数
时函数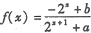 是奇函数.
是奇函数.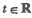 ,不等式
,不等式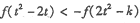 恒成立,求k的取值范围.
恒成立,求k的取值范围.
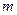 满足不等式
满足不等式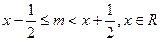 ,则称
,则称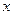 的“亲密整数”,记作
的“亲密整数”,记作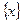 ,即
,即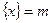 ,已知函数
,已知函数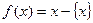 .给出以下四个命题:
.给出以下四个命题: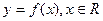 是周期函数且其最小正周期为
是周期函数且其最小正周期为 1;
1;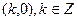 中心对称;
中心对称;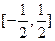 上单调递增;
上单调递增;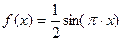 在
在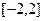 上共有7个不相等的实数根.
上共有7个不相等的实数根.
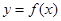 的大致图象如图所示,则函数
的大致图象如图所示,则函数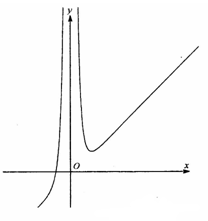
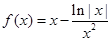
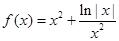
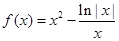
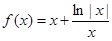
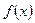 的图像关于直线
的图像关于直线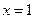 对称,且
对称,且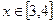 时,
时,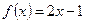 , 则
, 则 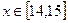 时,函数
时,函数