题目内容
已知二次函数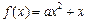 ,
,
(1)当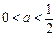 时,
时,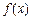 在 [ – 1,1 ] 上的最大值为
在 [ – 1,1 ] 上的最大值为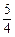 ,求
,求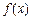 的最小值;
的最小值;
(2)对于任意的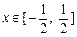 ,总有
,总有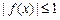 ,求a的取值范围;
,求a的取值范围;
(3)若当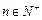 时,记
时,记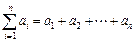 ,令a = 1,求证:
,令a = 1,求证: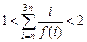 成立.
成立.
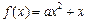 ,
,(1)当
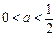 时,
时,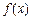 在 [ – 1,1 ] 上的最大值为
在 [ – 1,1 ] 上的最大值为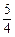 ,求
,求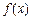 的最小值;
的最小值;(2)对于任意的
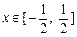 ,总有
,总有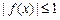 ,求a的取值范围;
,求a的取值范围;(3)若当
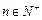 时,记
时,记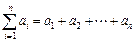 ,令a = 1,求证:
,令a = 1,求证: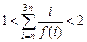 成立.
成立.(1) (2)
(2)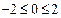 且
且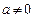 (3)见解析
(3)见解析
 (2)
(2)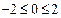 且
且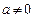 (3)见解析
(3)见解析(1) 由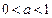 知
知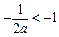 ,当x = 1时,解得最大值为
,当x = 1时,解得最大值为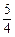 ,即
,即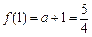
∴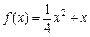 ∴
∴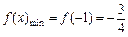
(2) 由题意知:当 t = 0时,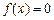 使
使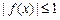 成立
成立
当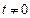 时,有
时,有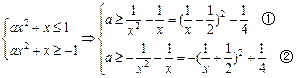
对任意的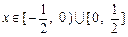 恒成立
恒成立
∵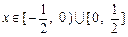
∴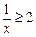 或
或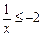 ,则
,则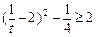
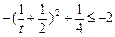 要使①②成立,则
要使①②成立,则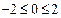
而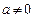 ,综上所述,
,综上所述,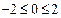 且
且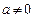
(3) 由题意: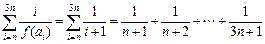
令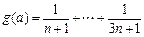
∴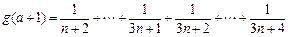
∴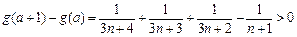
∴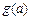 在
在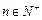 个
个
∴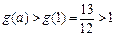
又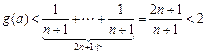
∴原结论成立
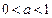 知
知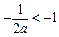 ,当x = 1时,解得最大值为
,当x = 1时,解得最大值为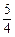 ,即
,即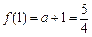
∴
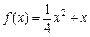 ∴
∴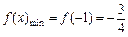
(2) 由题意知:当 t = 0时,
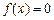 使
使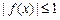 成立
成立当
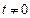 时,有
时,有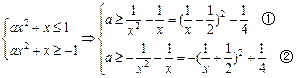
对任意的
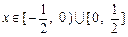 恒成立
恒成立∵
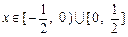
∴
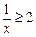 或
或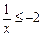 ,则
,则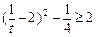
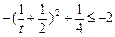 要使①②成立,则
要使①②成立,则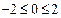
而
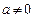 ,综上所述,
,综上所述,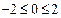 且
且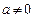
(3) 由题意:
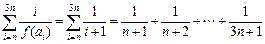
令
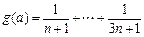
∴
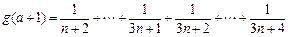
∴
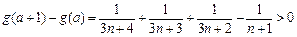
∴
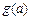 在
在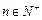 个
个∴
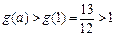
又
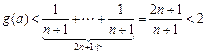
∴原结论成立

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
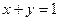 ,求
,求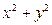 的最小值。
的最小值。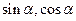 是方程
是方程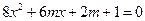 的两个实数根,求实数
的两个实数根,求实数 的值.
的值.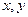

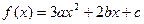 ,若a+b+c=0,f(0)f(1)>0,
,若a+b+c=0,f(0)f(1)>0,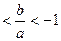 ;
;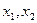 是方程f(x)=0的两个根,求
是方程f(x)=0的两个根,求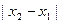 的取值范围
的取值范围
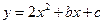 在
在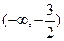 上是减函数,在
上是减函数,在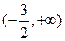 上是增函数,且两个零点
上是增函数,且两个零点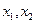 满足
满足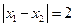 ,求二次函数的解析式。
,求二次函数的解析式。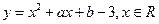 的图像恒过点(2,0),则
的图像恒过点(2,0),则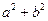 的最小值为
的最小值为 