题目内容
设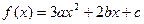 ,若a+b+c=0,f(0)f(1)>0,
,若a+b+c=0,f(0)f(1)>0,
(1)求证:方程f(x)=0有实根;
(2)求证:-2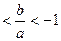 ;
;
(3)设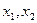 是方程f(x)=0的两个根,求
是方程f(x)=0的两个根,求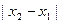 的取值范围
的取值范围
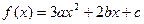 ,若a+b+c=0,f(0)f(1)>0,
,若a+b+c=0,f(0)f(1)>0,(1)求证:方程f(x)=0有实根;
(2)求证:-2
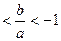 ;
;(3)设
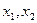 是方程f(x)=0的两个根,求
是方程f(x)=0的两个根,求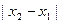 的取值范围
的取值范围 (1)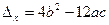 >0,所以所给方程有实根;(2)解此不等式得:-2
>0,所以所给方程有实根;(2)解此不等式得:-2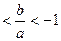 ;(3)
;(3) 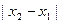
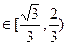
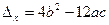 >0,所以所给方程有实根;(2)解此不等式得:-2
>0,所以所给方程有实根;(2)解此不等式得:-2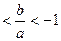 ;(3)
;(3) 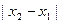
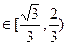
f(0)f(1)>0 c(3a+2b+c)>0, 又a+b+c="0" 即c=-a-b
c(3a+2b+c)>0, 又a+b+c="0" 即c=-a-b
所以(-a-b)(2a+b)>0即 2a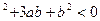
(1)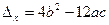 =4
=4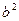 +12a(a+b)=12a
+12a(a+b)=12a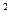 +12ab+4b
+12ab+4b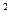
=12[(a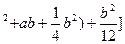 >0
>0
所以所给方程有实根。;
(2)由2a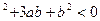 知
知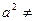 0,
0,
且
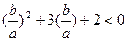 解此不等式得:-2
解此不等式得:-2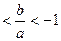
(3)|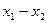 |=
|=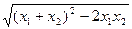 =
=
=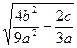
= -2
-2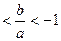
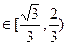
 c(3a+2b+c)>0, 又a+b+c="0" 即c=-a-b
c(3a+2b+c)>0, 又a+b+c="0" 即c=-a-b所以(-a-b)(2a+b)>0即 2a
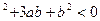
(1)
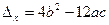 =4
=4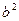 +12a(a+b)=12a
+12a(a+b)=12a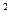 +12ab+4b
+12ab+4b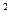
=12[(a
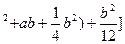 >0
>0
所以所给方程有实根。;
(2)由2a
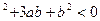 知
知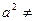 0,
0,且

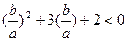 解此不等式得:-2
解此不等式得:-2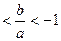
(3)|
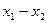 |=
|=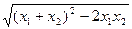 =
==
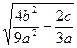
=
 -2
-2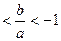

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
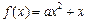 ,
,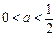 时,
时,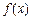 在 [ – 1,1 ] 上的最大值为
在 [ – 1,1 ] 上的最大值为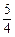 ,求
,求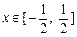 ,总有
,总有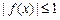 ,求a的取值范围;
,求a的取值范围;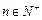 时,记
时,记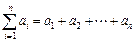 ,令a = 1,求证:
,令a = 1,求证: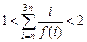 成立.
成立.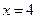 ;
;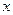 轴两个交点的横坐标都是整数;
轴两个交点的横坐标都是整数;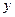 轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为
轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为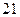 .
.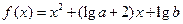 满足
满足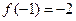 ,且对一切实数
,且对一切实数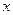 都有
都有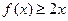 ,求实数
,求实数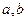 的值.
的值.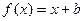 的图象与函数
的图象与函数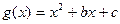 的图象相切.
的图象相切. 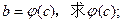
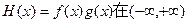 内有极值点?若存在,求出c的取值范围;若不存在,请说明理由.
内有极值点?若存在,求出c的取值范围;若不存在,请说明理由. 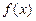 满足
满足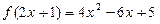 ,求
,求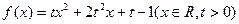
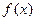 的最小值
的最小值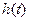 ;
;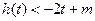 对
对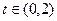 恒成立,求实数
恒成立,求实数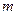 的取值范围。
的取值范围。