题目内容
2．直线y=x+2被圆M：x2+y2-4x-4y-1=0所截得的弦长为$2\sqrt{7}$．分析 先求出圆心到直线的距离既得弦心距，求出圆的半径，利用勾股定理求出弦长的一半，即可求得弦长
解答 解：x2+y2-4x-4y-1=0可变为（x-2）2+（y-2）2=9，故圆心坐标为（2，2），半径为3．
圆心到直线x-y+2=0的距离是$\frac{2}{\sqrt{2}}$=$\sqrt{2}$，
故弦长的一半是$\sqrt{9-2}$=$\sqrt{7}$
所以弦长为$2\sqrt{7}$．
故答案为：$2\sqrt{7}$．
点评 本题考查直线与圆相交的性质，解题的关键是了解直线与圆相交的性质，半径，弦心距，弦长的一半构成一个直角三角形，掌握点到直线的公式，会用它求点直线的距离．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
12．如图是某算法的程序框图，若程序运行后输出的结果是27，则判断框①处应填入的条件是（ ）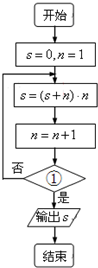
| A． | n＞2 | B． | n＞3 | C． | n＞4 | D． | n＞5 |
17．已知实数x，y满足平面区域$D：\left\{\begin{array}{l}x+y-1≥0\\ 2x-y-2≤0\\ x-2y+2≥0\end{array}\right.$，则x2+y2的最大值为（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $2\sqrt{2}$ | D． | 8 |
11．若曲线C1：x2+y2-2x=0与曲线C2：y（y-mx-m）=0有四个不同的交点，则实数m的取值范围是（ ）
| A． | （-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$） | B． | （-∞，-$\frac{\sqrt{3}}{3}$）∪（$\frac{\sqrt{3}}{3}$，+∞） | C． | [-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$] | D． | （-$\frac{\sqrt{3}}{3}$，0）∪（0，$\frac{\sqrt{3}}{3}$） |
如图，四边形ABCD为平行四边形，AB=5，AD=4，BD=3，将△BCD沿着BD翻折到平面BC1D处，E，F分别为边AB，C1D的中点．