题目内容
7.已知函数f(x)=sinx.若存在x1,x2,…,xm满足0≤x1<x2<…<xm≤6π,且|f(x1)-f(x2)|+|f(x2)-f(x3)|+…+|f(xm-1)-f(xm)|=12(m≥2,m∈N*),则m的最小值为8.分析 由正弦函数的有界性可得,对任意xi,xj(i,j=1,2,3,…,m),都有|f(xi)-f(xj)|≤f(x)max-f(x)min=2,要使m取得最小值,尽可能多让xi(i=1,2,3,…,m)取得最高点,然后作图可得满足条件的最小m值.
解答 解:∵y=sinx对任意xi,xj(i,j=1,2,3,…,m),都有|f(xi)-f(xj)|≤f(x)max-f(x)min=2,
要使m取得最小值,尽可能多让xi(i=1,2,3,…,m)取得最高点,
考虑0≤x1<x2<…<xm≤6π,|f(x1)-f(x2)|+|f(x2)-f(x3)|+…+|f(xm-1)-f(xm)|=12,
按下图取值即可满足条件,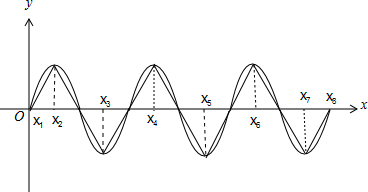
∴m的最小值为8.
故答案为:8.
点评 本题考查正弦函数的图象和性质,考查分析问题和解决问题的能力,考查数学转化思想方法,正确理解对任意xi,xj(i,j=1,2,3,…,m),都有|f(xi)-f(xj)|≤f(x)max-f(x)min=2是解答该题的关键,是难题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
17.等差数列{an}中,若a4+a8=-3,则a6(a2+2a6+a10)的值是( )
| A. | -9 | B. | 9 | C. | -6 | D. | 3 |
15.若?x∈[$\frac{1}{4}$,+∞),使得不等式ex<$\frac{x-m}{\sqrt{x}}$成立,则实数m的取值范围是( )
| A. | (-∞,-$\frac{1}{2}$${e}^{\frac{1}{4}}$) | B. | ($\frac{1}{4}$-$\frac{1}{2}$${e}^{\frac{1}{4}}$,+∞) | C. | (-∞,$\frac{1}{4}$-$\frac{1}{2}$${e}^{\frac{1}{4}}$) | D. | ($\frac{1}{2}$-$\frac{1}{2}$${e}^{\frac{1}{4}}$,+∞) |
19.若函数f(x)=$\left\{\begin{array}{l}{x^2}-5x,x≥0\\-{x^2}+ax,x<0\end{array}$是奇函数,则实数a的值是( )
| A. | -10 | B. | 10 | C. | -5 | D. | 5 |
17.若sinxcosy+cosxsiny=$\frac{1}{2}$,cos2x-cos2y=$\frac{2}{3}$,则sin(x-y)等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |