题目内容
17.已知实数x,y满足平面区域$D:\left\{\begin{array}{l}x+y-1≥0\\ 2x-y-2≤0\\ x-2y+2≥0\end{array}\right.$,则x2+y2的最大值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $2\sqrt{2}$ | D. | 8 |
分析 作出不等式组对应的平面区域,利用z的几何意义进行求解即可.
解答 解:作出不等式组对应的平面区域如图;
设z=x2+y2的,
则z的几何意义是区域内的点到原点的距离的平方,
由图象知,OA的距离最大,
由$\left\{\begin{array}{l}{2x-y-2=0}\\{x-2y+2=0}\end{array}\right.$得 $\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
即A(2,2),
即z=x2+y2的最大值为z=22+22=4+4=8,
故选:D
点评 本题主要考查线性规划以及点到直线的距离的应用,利用数形结合是解决本题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
7.若复数z满足(4-3i)z=|3+4i|,则z的虚部为( )
| A. | $\frac{3}{5}$i | B. | $\frac{3}{5}$ | C. | 3 | D. | 3i |
9.若无重复数字的三位数满足条件:①个位数字与十位数字之和为奇数,②所有位的数字和为偶数.则这样的三位数的个数是( )
| A. | 540 | B. | 480 | C. | 360 | D. | 200 |
6.某几何体三视图如下,图中三个等腰三角形的直角边长都是2,该几何体的体积为( )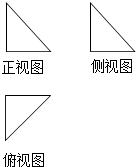

| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
7.执行如图所示的程序框图,则输出的i的值是( )
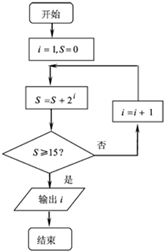

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD 是以AD为底的等腰三角形.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD 是以AD为底的等腰三角形. 如图,已知直三棱柱ABC-A1B1C1中,AA1=AB=AC,AB⊥AC,M,N,Q分别是CC1,BC,AC的中点,点P在线段A1B1上运动.
如图,已知直三棱柱ABC-A1B1C1中,AA1=AB=AC,AB⊥AC,M,N,Q分别是CC1,BC,AC的中点,点P在线段A1B1上运动.