题目内容
14.已知函数f(x)=ax-ln(x+b)在点(1,1)处的切线与x轴平行.(1)求实数a,b的值;
(2)证明:$\sum_{k=2}^n\frac{1}{k-f(k)}>\frac{{3{n^2}-n-2}}{n(n+1)}$(n∈N,n≥2).
分析 (1)求导数,利用f′(1)=0,f(1)=a-lnb=1,即可求实数a,b的值;
(2)k-f(k)=lnk,设$h(x)=\frac{{{x^2}-1}}{4}-lnx(x≥2)$,则$h′(x)=\frac{x}{2}-\frac{1}{x}=\frac{{{x^2}-2}}{2}>0$恒成立,即h(x)在[2,+∞)上是增函数,bn>an等价于$\frac{1}{{a}_{n}}-\frac{1}{{b}_{n}}$≥$\frac{1}{{a}_{2}}$-$\frac{1}{{b}_{2}}$=h(2)=$\frac{3}{4}$-ln2>0,即可证明结论.
解答 解:(1)∵$f′(x)=a-\frac{1}{x+b}$,又由已知得f′(1)=0①f(1)=a-lnb=1②
由①,②解得:a=1,b=0
(2)k-f(k)=lnk,设${b_n}=lnn,{T_n}=\frac{{3{n^2}-n-2}}{n(n+1)},{a_n}={T_n}-{T_{n-1}}=\frac{4}{{{n^2}-1}}$
当n≥2时有,$\frac{1}{a_n}=\frac{{{n^2}-1}}{4}>0,{b_n}=lnn>0$
设$h(x)=\frac{{{x^2}-1}}{4}-lnx(x≥2)$,则$h′(x)=\frac{x}{2}-\frac{1}{x}=\frac{{{x^2}-2}}{2}>0$恒成立
即h(x)在[2,+∞)上是增函数,
∴bn>an等价于$\frac{1}{{a}_{n}}-\frac{1}{{b}_{n}}$≥$\frac{1}{{a}_{2}}$-$\frac{1}{{b}_{2}}$=h(2)=$\frac{3}{4}$-ln2>0,
∴$\frac{1}{ln2}$+$\frac{1}{ln3}$+…+$\frac{1}{lnn}$>$\frac{4}{3}$+$\frac{4}{8}$+…+$\frac{4}{{n}^{2}-1}$=$\frac{3{n}^{2}-n-2}{n(n+1)}$,
∴$\sum_{k=2}^n\frac{1}{k-f(k)}>\frac{{3{n^2}-n-2}}{n(n+1)}$(n∈N,n≥2).
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.

| A. | 540 | B. | 480 | C. | 360 | D. | 200 |
| A. | -10 | B. | 10 | C. | -5 | D. | 5 |
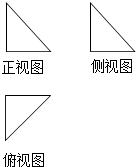
| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |