题目内容
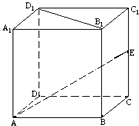
在正方体ABCD-A1B1C1D1中，O为AC，BD的交点，则C1O与A1D所成角余弦（ ）
A．
| B．0 | C．
| D．
|
设正方体ABCD-A1B1C1D1的棱长为2，以DA为x轴，以DC为y轴，以DD1为z轴，建立空间直角坐标系，
则C1（0，2，2），O（1，1，0），A1（2，0，2），D（0，0，0），
∴
=（1，-1，-2），
=（-2，0，-2），
设C1O与A1D所成角为θ，
则cosθ=|cos＜
，
|=|
|=
．
故选C．
则C1（0，2，2），O（1，1，0），A1（2，0，2），D（0，0，0），
∴
| C1O |
| A1D |
设C1O与A1D所成角为θ，
则cosθ=|cos＜
| C1O |
| A1D |
| -2+0+4 | ||||
|
| ||
| 6 |
故选C．
练习册系列答案
名校课堂系列答案
相关题目
