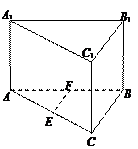题目内容
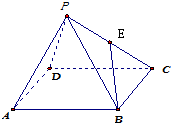
如图，边长为2的正方形ABCD外有一点P，且PA=PB=PC=PD=2中，E是PC的中点．
（1）求证：PA∥平面EBD；
（2）求异面直线PA与BE所成的角的余弦值．
（1）求证：PA∥平面EBD；
（2）求异面直线PA与BE所成的角的余弦值．
（1）取BD中点O，连接OE，
∵四边形ABCD是正方形，
∴AO=OC．
又PE=EC，
∴OE∥PA．
又AP?平面EBD，OE?平面EBD．
∴PA∥平面EBD；
（2）由（1）可知：PA∥EO，
∴∠OEB是异面直线PA与BE所成的角．
∵正方形ABCD的边长为2，且PA=PB=PC=PD=2，E为PC的中点．
∴OB=
BD=
×2
=
，EB=
，
在Rt△OBE中，OE=
=1．
∴cos∠OEB=
=
．
∵四边形ABCD是正方形，
∴AO=OC．
又PE=EC，
∴OE∥PA．
又AP?平面EBD，OE?平面EBD．
∴PA∥平面EBD；
（2）由（1）可知：PA∥EO，
∴∠OEB是异面直线PA与BE所成的角．
∵正方形ABCD的边长为2，且PA=PB=PC=PD=2，E为PC的中点．
∴OB=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
在Rt△OBE中，OE=
| EB2-OB2 |
∴cos∠OEB=
| OE |
| EB |
| ||
| 3 |
练习册系列答案
名校课堂系列答案
相关题目
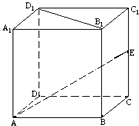
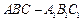中，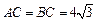
，
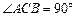，AA1=2，E、F分别是AC、AB的中点，过直线EF作棱柱的截面，若截面与平面ABC所成的二面角的大小为
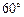，则截面的面积为____________.
