题目内容
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 左、右焦点,点
左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)![]() 是椭圆
是椭圆![]() 上异于点
上异于点![]() 的两个动点,如果直线
的两个动点,如果直线![]() 与直线
与直线![]() 的倾斜角互补,证明:直线
的倾斜角互补,证明:直线![]() 的斜率为定值,并求出这个定值.
的斜率为定值,并求出这个定值.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)根据点![]() 在椭圆上,以及
在椭圆上,以及![]() 轴,可以求出
轴,可以求出![]() 的值,再根据
的值,再根据![]() 的周长为
的周长为![]() 以及椭圆的定义可以求出
以及椭圆的定义可以求出![]() ,进而可以得到椭圆的标准方程;(2)根据题目条件可知直线
,进而可以得到椭圆的标准方程;(2)根据题目条件可知直线![]() 与直线
与直线![]() 的斜率应是互为相反数,据此可以得到点
的斜率应是互为相反数,据此可以得到点![]() 坐标,进而可以求出直线
坐标,进而可以求出直线![]() 的斜率为定值,即证明了直线
的斜率为定值,即证明了直线![]() 的斜率为定值.
的斜率为定值.
试题解析:(1)由题意,![]() ,...............1分
,...............1分
![]() …………… 2分
…………… 2分
∴![]() ............3分
............3分
∴ 椭圆方程为![]() ,..........................4分
,..........................4分
(2)由(1)知![]() ,设直线
,设直线![]() 方程:得
方程:得![]() ,代入
,代入![]() 得
得
 .....................6分
.....................6分
设![]() ,因为点
,因为点![]() 在椭圆上,所以
在椭圆上,所以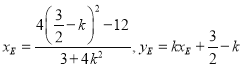 ,
,
又直线![]() 的斜率与
的斜率与![]() 的斜率互为相反数,在上式中以
的斜率互为相反数,在上式中以![]() 代
代![]() ,可得
,可得
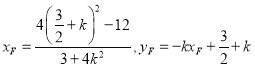 ...................9分
...................9分
所以直线![]() 的斜率
的斜率![]() ,
,
即直线![]() 的斜率为定值,其值为
的斜率为定值,其值为![]() .......................10分
.......................10分

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目