题目内容
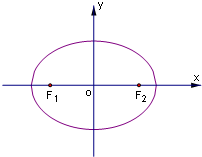
过椭圆
+y2=1的左焦点F1的直线l交椭圆于A、B两点.
(1)求
•
的范围;
(2)若
⊥
,求直线l的方程.

| x2 |
| 2 |
(1)求
| AO |
| AF1 |
(2)若
| OA |
| OB |

(1)∵椭圆
+y2=1,
∴a=
,b=1,c=1,
∴F1(-1,0),…(1分)
设A(x1,y1),则
•
=
+x1+
…(3分)
∵
+y12=1,
∴
•
=
+x1+
=
+x1+1=
(x1+1)2+
…(5分)
∵x1∈[-
,
],
∴
•
∈[
,
+2],…(6分)
(2)设A、B两点的坐标为A(x1,y1)、B(x2,y2)
①当l平行于y轴时,点A(-1,
)、B(-1,-
),此时
•
=
≠0…(8分)
②当l不平行于y轴时,设直线l的斜率为k,则直线l方程为y=k(x+1),
由
得(1+2k2)x2+4k2x+2k2-2=0…(9分)
∴x1+x2=-
,x1x2=
…(11分)
∴
•
=x1x2+y1y2=(1+k2)x1x2+k2(x1+x2)+k2
=(1+k2)•
-k2•
+k2=0
解得k2=2,
∴k=±
…(13分)
故所求的直线方程为y=±
(x+1)…(14分)
| x2 |
| 2 |
∴a=
| 2 |
∴F1(-1,0),…(1分)
设A(x1,y1),则
| AO |
| AF1 |
| x | 21 |
| y | 21 |
∵
| x12 |
| 2 |
∴
| AO |
| AF1 |
| x | 21 |
| y | 21 |
| 1 |
| 2 |
| x | 21 |
| 1 |
| 2 |
| 1 |
| 2 |
∵x1∈[-
| 2 |
| 2 |
∴
| AO |
| AF1 |
| 1 |
| 2 |
| 2 |
(2)设A、B两点的坐标为A(x1,y1)、B(x2,y2)
①当l平行于y轴时,点A(-1,
| ||
| 2 |
| ||
| 2 |
| OA |
| OB |
| 1 |
| 2 |
②当l不平行于y轴时,设直线l的斜率为k,则直线l方程为y=k(x+1),
由
|
∴x1+x2=-
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
∴
| OA |
| OB |
=(1+k2)•
| 2k2-2 |
| 1+2k2 |
| 4k2 |
| 1+2k2 |
解得k2=2,
∴k=±
| 2 |
故所求的直线方程为y=±
| 2 |

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 O外一点,PA是切线,A为切点,割线PBC与
O外一点,PA是切线,A为切点,割线PBC与
 DE=2
DE=2



 的直径
的直径 ,
, 是
是 延长线上的一点,过
延长线上的一点,过 ,连接
,连接 ,若
,若 ,
,
 .
.