题目内容
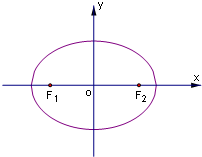
如图,设点F1(-c,0)、F2(c,0)分别是椭圆C:
+y2=1(a>1)的左、右焦点,P为椭圆C上任意一点,且
•
最小值为0.
(1)求椭圆C的方程;
(2)设直线l1:y=kx+m,l2:y=kx+n,若l1、l2均与椭圆C相切,证明:m+n=0;
(3)在(2)的条件下,试探究在x轴上是否存在定点B,点B到l1,l2的距离之积恒为1?若存在,请求出点B坐标;若不存在,请说明理由.
| x2 |
| a2 |
| PF1 |
| PF2 |
(1)求椭圆C的方程;
(2)设直线l1:y=kx+m,l2:y=kx+n,若l1、l2均与椭圆C相切,证明:m+n=0;
(3)在(2)的条件下,试探究在x轴上是否存在定点B,点B到l1,l2的距离之积恒为1?若存在,请求出点B坐标;若不存在,请说明理由.

(1)设P(x,y),则有
=(-c-x,-y),
=(c-x,-y).
•
=x2+y2-c2=
x2+1-c2,x∈[-a,a].
由
•
最小值为0,得1-c2=0,所以c=1,则a2=b2+c2=1+1=2,
∴椭圆C的方程为
+y2=1;
(2)把y=kx+m代入椭圆
+y2=1,得(1+2k2)x2+4mkx+2m2-2=0,
∵直线l1与椭圆C相切,∴△=16k2m2-4(1+2k2)(2m2-2)=0,化简得m2=1+2k2,
把y=kx+n代入椭圆
+y2=1,得(1+2k2)x2+4nkx+2n2-2=0,
∵直线l2与椭圆C相切,∴△=16k2n2-4(1+2k2)(2n2-2)=0,化简得n2=1+2k2,
∴m2=n2,若m=n,则l1,l2重合,不合题意,
∴m=-n,即m+n=0;
(3)设在x轴上存在点B(t,0),点B到直线l1,l2的距离之积为1,
则
•
=1,即|k2t2-m2|=k2+1,
把1+2k2=m2代入并去绝对值整理,得k2(t2-3)=2或k2(t2-1)=0,
k2(t2-3)=2不满足对任意的k∈R恒成立;而要使得k2(t2-1)=0对任意的k∈R恒成立
则t2-1=0,解得t=±1;
综上所述,满足题意的定点B存在,其坐标为(-1,0)或(1,0).
| PF1 |
| PF2 |
| PF1 |
| PF2 |
| a2-1 |
| a2 |
由
| PF1 |
| PF2 |
∴椭圆C的方程为
| x2 |
| 2 |
(2)把y=kx+m代入椭圆
| x2 |
| 2 |
∵直线l1与椭圆C相切,∴△=16k2m2-4(1+2k2)(2m2-2)=0,化简得m2=1+2k2,
把y=kx+n代入椭圆
| x2 |
| 2 |
∵直线l2与椭圆C相切,∴△=16k2n2-4(1+2k2)(2n2-2)=0,化简得n2=1+2k2,
∴m2=n2,若m=n,则l1,l2重合,不合题意,
∴m=-n,即m+n=0;
(3)设在x轴上存在点B(t,0),点B到直线l1,l2的距离之积为1,
则
| |kt+m| | ||
|
| |kt-m| | ||
|
把1+2k2=m2代入并去绝对值整理,得k2(t2-3)=2或k2(t2-1)=0,
k2(t2-3)=2不满足对任意的k∈R恒成立;而要使得k2(t2-1)=0对任意的k∈R恒成立
则t2-1=0,解得t=±1;
综上所述,满足题意的定点B存在,其坐标为(-1,0)或(1,0).

练习册系列答案
相关题目
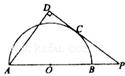
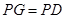 ,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.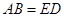 .
.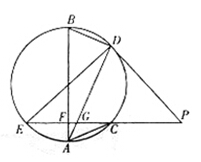
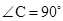 , BE平分∠ABC交AC于点E, 点D在AB上,
, BE平分∠ABC交AC于点E, 点D在AB上,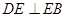 .
.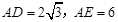 ,求EC的长.
,求EC的长.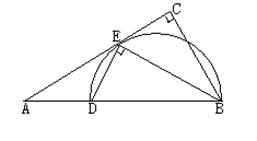

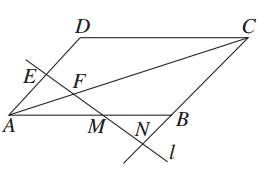
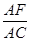 =________.
=________.
 PD.若PC=4, PB=2,则CD=____________.
PD.若PC=4, PB=2,则CD=____________.