题目内容
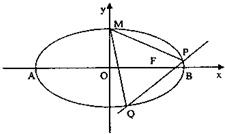
如图,设椭圆
+
=1(a>b>0)长轴的右端点为A,短轴端点分别为B、C,另有抛物线y=x2+b.
(Ⅰ)若抛物线上存在点D,使四边形ABCD为菱形,求椭圆的方程;
(Ⅱ)若a=2,过点B作抛物线的切线,切点为P,直线PB与椭圆相交于另一点Q,求
的取值范围.

| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)若抛物线上存在点D,使四边形ABCD为菱形,求椭圆的方程;
(Ⅱ)若a=2,过点B作抛物线的切线,切点为P,直线PB与椭圆相交于另一点Q,求
| |PQ| |
| |QB| |

(Ⅰ)由四边形ABCD是菱形,得D(a,a2+b),
且
,解得a=
,b=
,
所以椭圆方程为3x2+9y2=1.
(Ⅱ)不妨设P(t,t2+b)(t≠0),
因为y'|x=t=2x|x=t=2t,
所以PQ的方程为y=2t(x-t)+t2+b,即y=2tx-t2+b.
又因为直线PQ过点B,所以-t2+b=-b,即b=
.
所以PQ的方程为y=2tx-
.
联立方程组
,消去y,得(t2+64)x2-32tx=0.
所以点Q的横坐标为xQ=
,
所以
=
=
+1.
又t2=2b∈(0,4),所以
的取值范围为(1,
).

且
|
| ||
| 3 |
| 1 |
| 3 |
所以椭圆方程为3x2+9y2=1.
(Ⅱ)不妨设P(t,t2+b)(t≠0),
因为y'|x=t=2x|x=t=2t,
所以PQ的方程为y=2t(x-t)+t2+b,即y=2tx-t2+b.
又因为直线PQ过点B,所以-t2+b=-b,即b=
| t2 |
| 2 |
所以PQ的方程为y=2tx-
| t2 |
| 2 |
联立方程组
|
所以点Q的横坐标为xQ=
| 32t |
| t2+64 |
所以
| |PQ| |
| |QB| |
| xP-xQ |
| xQ-xB2 |
| t2 |
| 32 |
又t2=2b∈(0,4),所以
| |PQ| |
| |QB| |
| 9 |
| 8 |


练习册系列答案
相关题目
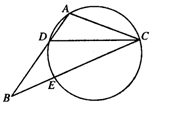



 中,
中, ,以
,以 为直径的半圆分别交
为直径的半圆分别交 于点
于点 ,若
,若 ,则
,则 =_______.
=_______.