题目内容
已知抛物线C的方程为:y2=4x,直线l过(-2,1)且斜率为k≥0,当k为何值时,直线l与抛物线C(1)只有一个公共点,(2)有两个公共点.
(1)当k=0时,直线l的方程为y=1,与抛物线C的方程联立
,解得(
,1),此时直线l与抛物线C只有一个公共点.
k>0时,直线l的方程为y-1=k(x+2),联立
,化为k2x2+(4k2+2k-4)x+(2k+1)2=0,
当直线l与抛物线相切时,△=(4k2+2k-4)2-4k2(2k+1)2=0,化为2k2+k-1=0,解得k=-1或
.
即当k=-1或
时,直线l与抛物线C只有一个公共点.
综上可知:当k=0,-1或
时,直线l与抛物线C只有一个公共点.
(2)k>0时,直线l的方程为y-1=k(x+2),联立
,化为k2x2+(4k2+2k-4)x+(2k+1)2=0,
当直线l与抛物线相交时,△=(4k2+2k-4)2-4k2(2k+1)2>0,化为2k2+k-1<0,解得-1<k<
.
故当-1<k<
且k≠0时,直线l与抛物线相交于两个交点.
|
| 1 |
| 4 |
k>0时,直线l的方程为y-1=k(x+2),联立
|
当直线l与抛物线相切时,△=(4k2+2k-4)2-4k2(2k+1)2=0,化为2k2+k-1=0,解得k=-1或
| 1 |
| 2 |
即当k=-1或
| 1 |
| 2 |
综上可知:当k=0,-1或
| 1 |
| 2 |
(2)k>0时,直线l的方程为y-1=k(x+2),联立
|
当直线l与抛物线相交时,△=(4k2+2k-4)2-4k2(2k+1)2>0,化为2k2+k-1<0,解得-1<k<
| 1 |
| 2 |
故当-1<k<
| 1 |
| 2 |

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
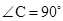 , BE平分∠ABC交AC于点E, 点D在AB上,
, BE平分∠ABC交AC于点E, 点D在AB上,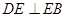 .
.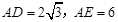 ,求EC的长.
,求EC的长.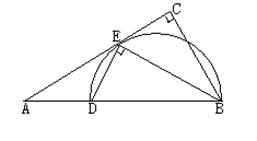


 中,
中, ,
, ,若
,若 ,
, ,
, ,则
,则 的长为_______.
的长为_______.