题目内容
如图,P是 O外一点,PA是切线,A为切点,割线PBC与
O外一点,PA是切线,A为切点,割线PBC与 O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交
O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交 O于点E。
O于点E。

证明:(1)BE=EC;
(2)AD DE=2
DE=2
 O外一点,PA是切线,A为切点,割线PBC与
O外一点,PA是切线,A为切点,割线PBC与 O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交
O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交 O于点E。
O于点E。
证明:(1)BE=EC;
(2)AD
 DE=2
DE=2
(1)见解析 (2)见解析
试题分析:本题第(1)问,先由已知得出PA=PD,然后由对应角相等,拆分角得出结论;对第(2)问,可由切割线定理得出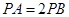 ,
,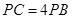 ,
,
然后由相交弦定理,得出结论.
试题解析:(1)连结AB,AC,由题意知PA=PD,故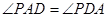 ,因为
,因为 ,
,
 ,
,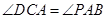 ,所以
,所以 ,从而
,从而 ,因此BE=EC.
,因此BE=EC.
(2)由切割线定理得: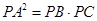 ,因为
,因为 ,所以
,所以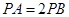 ,
,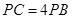 ,
,
由相交弦定理得: =
= =
=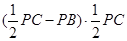
=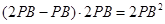 ,所以等式成立.
,所以等式成立.
【易错点】对第(1)问,不容易找到思路;第(2)问中不会灵活应用已知条件而出错.
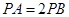 ,
,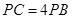 ,
,然后由相交弦定理,得出结论.
试题解析:(1)连结AB,AC,由题意知PA=PD,故
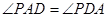 ,因为
,因为 ,
, ,
,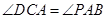 ,所以
,所以 ,从而
,从而 ,因此BE=EC.
,因此BE=EC.(2)由切割线定理得:
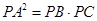 ,因为
,因为 ,所以
,所以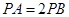 ,
,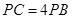 ,
,由相交弦定理得:
 =
= =
=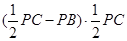
=
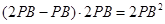 ,所以等式成立.
,所以等式成立.【易错点】对第(1)问,不容易找到思路;第(2)问中不会灵活应用已知条件而出错.

练习册系列答案
相关题目
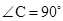 , BE平分∠ABC交AC于点E, 点D在AB上,
, BE平分∠ABC交AC于点E, 点D在AB上,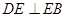 .
.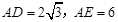 ,求EC的长.
,求EC的长.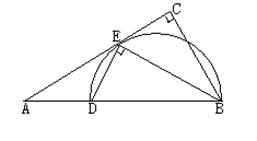

 中,
中, ,以
,以 为直径的半圆分别交
为直径的半圆分别交 于点
于点 ,若
,若 ,则
,则 =_______.
=_______.
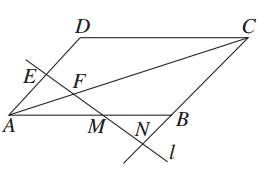
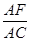 =________.
=________.

 __________
__________
 中,
中, ,
, ,若
,若 ,
, ,
, ,则
,则 的长为_______.
的长为_______.