题目内容
已知函数f(x)=xsinx,对于[-
,
]上的任意x1,x2,有如下条件:
①
>
;②x1>x2;③x1>x2,且
>0.其中能使f(x1)>f(x2)恒成立的条件序号是______.(写出所有满足条件的序号)
| π |
| 2 |
| π |
| 2 |
①
| x | 21 |
| x | 22 |
| x1+x2 |
| 2 |
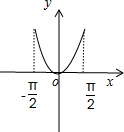
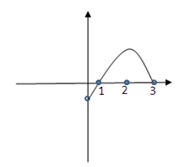
由已知得f(x)是偶函数,且在区间[-
,0]上递减,在[0,
]上递增,
作出函数的草图,如图所示:
由图象可知,f(x1)>f(x2)?|x1|>|x2|,即x12>x22.故①符合,②不符合;
由x1>x2,且
>0,知x1>0,
若x2>0,则显然f(x1)>f(x2)成立;
若x2<0,由x1+x2>0,得x1>-x2,
即|x1|>|x2|,有f(x1)>f(x2)成立,故③符合;
故答案为:①③.
| π |
| 2 |
| π |
| 2 |
作出函数的草图,如图所示:
由图象可知,f(x1)>f(x2)?|x1|>|x2|,即x12>x22.故①符合,②不符合;
由x1>x2,且
| x1+x2 |
| 2 |
若x2>0,则显然f(x1)>f(x2)成立;
若x2<0,由x1+x2>0,得x1>-x2,
即|x1|>|x2|,有f(x1)>f(x2)成立,故③符合;
故答案为:①③.


练习册系列答案
相关题目
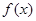 是定义在R上的奇函数,当
是定义在R上的奇函数,当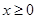 时
时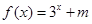 (m为常数),则
(m为常数),则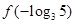 的值为( ).
的值为( ).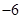
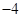
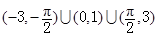
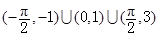
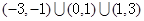
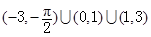
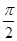 )=1,则f(-
)=1,则f(-