题目内容
已知函数f(x)=
,则f(1)+f(2)+f(3)+f(4)+f(5)+f(
)+f(
)+f(
)+f(
)=______.
| x2 |
| 1+x2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
∵f(x)=
,
∴f(x)+f(
)=
+
=
+
=
=1.
∴f(1)=
,
即f(1)+f(2)+f(3)+f(4)+f(5)+f(
)+f(
)+f(
)+f(
)=
+4[f(2)+f(
)]=
+4=
,
故答案为:
.
| x2 |
| 1+x2 |
∴f(x)+f(
| 1 |
| x |
| x2 |
| 1+x2 |
| ||
1+(
|
| x2 |
| 1+x2 |
| 1 |
| 1+x2 |
| 1+x2 |
| 1+x2 |
∴f(1)=
| 1 |
| 2 |
即f(1)+f(2)+f(3)+f(4)+f(5)+f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
故答案为:
| 9 |
| 2 |

练习册系列答案
相关题目

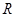 上的奇函数
上的奇函数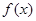 满足
满足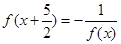 ,若
,若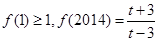 ,则实数
,则实数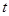 的取值范围为 .
的取值范围为 .