题目内容
数列{an}是等差数列的一个充要条件是(Sn是该数列前n项和)( )
| A、Sn=an+b |
| B、Sn=an2+bn+c |
| C、Sn=an2+bn (a≠0) |
| D、Sn=an2+bn |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:设Sn=an2+bn+c,由Sn求an的过程可得必要条件是:a≠0,c=0.只需再证明充分性即可,注意n的范围的限制.
解答:
解:设Sn=an2+bn+c
当n=1时,a1=a+b+c;当n≥2时,an=Sn-Sn-1=2an+b-a
由于a≠0,∴当n≥2时,{an}是公差为2a等差数列.
要使{an}是等差数列,则a2-a1=2a,解得c=0.
即{an}是等差数列的必要条件是:a≠0,c=0.
充分性:
当a≠0,c=0时Sn=an2+bn.
当n=1时,a1=a+b;当n≥2时,an=Sn-Sn-1=2an+b-a,
显然当n=1时也满足上式,
∴an=2an+b-a,进而可得an-an-1=2a,
∴{an}是等差数列.
综上可知,数列{an}是等差数列的充要条件是:Sn=an2+bn.
故选:C
当n=1时,a1=a+b+c;当n≥2时,an=Sn-Sn-1=2an+b-a
由于a≠0,∴当n≥2时,{an}是公差为2a等差数列.
要使{an}是等差数列,则a2-a1=2a,解得c=0.
即{an}是等差数列的必要条件是:a≠0,c=0.
充分性:
当a≠0,c=0时Sn=an2+bn.
当n=1时,a1=a+b;当n≥2时,an=Sn-Sn-1=2an+b-a,
显然当n=1时也满足上式,
∴an=2an+b-a,进而可得an-an-1=2a,
∴{an}是等差数列.
综上可知,数列{an}是等差数列的充要条件是:Sn=an2+bn.
故选:C
点评:本题考查等差数列的通项公式和求和公式的特点,涉及充要条件的证明,属中档题.

练习册系列答案
相关题目
 抛物线有光学性质,从焦点出发的光经抛物线反射后沿平行于抛物线的对称轴方向射出,今有抛物线y2=2px(p>0),一光源在点A(6,4)处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的B点,反射后,又射向抛物线上的C点,再反射后沿平行于抛物线的对称轴的方向射出,途中遇到直线l:x-y-7=0上的点D,再反射后又射回到A点,如图所示,则此抛物线的方程为( )
抛物线有光学性质,从焦点出发的光经抛物线反射后沿平行于抛物线的对称轴方向射出,今有抛物线y2=2px(p>0),一光源在点A(6,4)处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的B点,反射后,又射向抛物线上的C点,再反射后沿平行于抛物线的对称轴的方向射出,途中遇到直线l:x-y-7=0上的点D,再反射后又射回到A点,如图所示,则此抛物线的方程为( )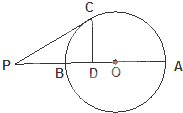 如图:AB是⊙O的直径,点P在AB的延长线上,且PB=OB=2,PC切⊙O于点C,CD⊥AB于点D,则CD=
如图:AB是⊙O的直径,点P在AB的延长线上,且PB=OB=2,PC切⊙O于点C,CD⊥AB于点D,则CD=