题目内容
已知函数f(x)=2
sinxcosx+cos2x-sin2x-1.
(1)若x∈[-π,π],求f(x)的单调增区间;
(2)若x∈[-
,
],求f(x)的取值范围;
(3)求函数的对称轴和对称中心.
| 3 |
(1)若x∈[-π,π],求f(x)的单调增区间;
(2)若x∈[-
| 5π |
| 12 |
| π |
| 3 |
(3)求函数的对称轴和对称中心.
考点:两角和与差的正弦函数,正弦函数的单调性,正弦函数的对称性
专题:计算题,三角函数的求值,三角函数的图像与性质
分析:(1)运用二倍角公式和两角和的正弦公式,化简f(x),再由正弦函数的单调增区间,解不等式,取k的值,即可得到所求;
(2)由x的范围,求得2x+
的范围,结合正弦函数的图象,即可得到所求f(x)的范围;
(3)运用正弦函数的对称轴方程和对称中心,解方程即可得到所求.
(2)由x的范围,求得2x+
| π |
| 6 |
(3)运用正弦函数的对称轴方程和对称中心,解方程即可得到所求.
解答:
解:(1)函数f(x)=2
sinxcosx+cos2x-sin2x-1
=
sin2x+cos2x-1=2(
sin2x+
cos2x)-1=2sin(2x+
)-1.
令2kπ-
≤2x+
≤2kπ+
,k∈Z,解得,kπ-
≤x≤kπ+
,
由于x∈[-π,π],则k=0,得-
≤x≤
,k=1得
≤x≤π,
k=-1,得,-π≤x≤-
,
即有f(x)的单调增区间为:[-
,
],[-π,-
],[
,π];
(2)由于x∈[-
,
],则2x+
∈[-
,
],
则sin(2x+
)∈[-1,1],则f(x)∈[-3,1],
则f(x)的取值范围:[-3,1];
(3)由于f(x)=2sin(2x+
)-1.
令2x+
=kπ+
,则x=
+
,k∈Z,
再令2x+
=kπ,解得,x=
-
,k∈Z,
即有函数的对称轴方程为:x=
+
,k∈Z,
对称中心为(
-
,-1),k∈Z.
| 3 |
=
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
由于x∈[-π,π],则k=0,得-
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
k=-1,得,-π≤x≤-
| 5π |
| 6 |
即有f(x)的单调增区间为:[-
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
| 2π |
| 3 |
(2)由于x∈[-
| 5π |
| 12 |
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
| 5π |
| 6 |
则sin(2x+
| π |
| 6 |
则f(x)的取值范围:[-3,1];
(3)由于f(x)=2sin(2x+
| π |
| 6 |
令2x+
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 6 |
再令2x+
| π |
| 6 |
| kπ |
| 2 |
| π |
| 6 |
即有函数的对称轴方程为:x=
| kπ |
| 2 |
| π |
| 6 |
对称中心为(
| kπ |
| 2 |
| π |
| 6 |
点评:本题考查三角函数的化简和求值,考查二倍角公式和两角和的正弦公式的运用,考查正弦函数的单调区间和正弦函数的对称轴和对称中心,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
数列{an}是等差数列的一个充要条件是(Sn是该数列前n项和)( )
| A、Sn=an+b |
| B、Sn=an2+bn+c |
| C、Sn=an2+bn (a≠0) |
| D、Sn=an2+bn |
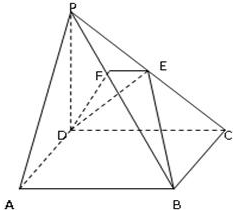 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ACD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ACD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.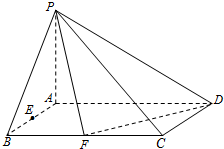 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.