题目内容
已知等差数列{an}中sn是它的前n项和,设a4=-2,s5=-20
(1)求数列{an}的通项公式;
(2)若bn=
,求数列{bn}的前n项.
(1)求数列{an}的通项公式;
(2)若bn=
| 1 |
| (an+10)(an+12) |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)根据已知条件建立方程组求出通项公式.
(2)首先利用(1)的结论求出新数列的通项公式,进一步利用裂项相消法求数列的和.
(2)首先利用(1)的结论求出新数列的通项公式,进一步利用裂项相消法求数列的和.
解答:
解:(1)等差数列{an}中sn是它的前n项和,设a4=-2,s5=-20
则:
解得:an=2n-10
(2)由(1)得到:bn=
=
=
(
-
)
Sn=b1+b2+…+bn
=
(1-
+
-
+…+
-
)
=
(1-
)=
则:
|
解得:an=2n-10
(2)由(1)得到:bn=
| 1 |
| (an+10)(an+12) |
| 1 |
| 4n(n+1) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
Sn=b1+b2+…+bn
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 1 |
| 4 |
| 1 |
| n+1 |
| n |
| 4n+4 |
点评:本题考查的知识要点:数列的通项公式的求法,利用裂项相消法求数列的和,属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列函数存在极值的是( )
A、y=
| ||
| B、y=x-ex | ||
| C、y=x3+x2+2x-3 | ||
| D、y=x3 |
设函数f(x)的定义域为M,若函数f(x)满足条件[m,n]⊆M,使f(x)在[m,n]上的值域是[
,
],则成f(x)为“半缩函数”,若函数f(x)=log3(3x+λ)为“半缩函数”,则λ的范围是( )
| m |
| 2 |
| n |
| 2 |
| A、(0,1) | ||
B、(0,
| ||
C、(0,
| ||
D、(
|
数列{an}是等差数列的一个充要条件是(Sn是该数列前n项和)( )
| A、Sn=an+b |
| B、Sn=an2+bn+c |
| C、Sn=an2+bn (a≠0) |
| D、Sn=an2+bn |
若函数f(x)=x3-mx2+mx+3m在(0,1)内有极大值,无极小值,则( )
| A、m<0 | B、m<3 |
| C、m>3 | D、0<m<3 |
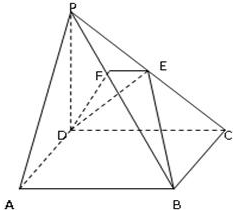 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ACD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ACD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.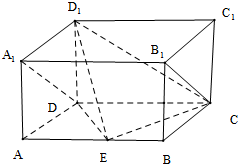 如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB的中点.
如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB的中点.