题目内容
 抛物线有光学性质,从焦点出发的光经抛物线反射后沿平行于抛物线的对称轴方向射出,今有抛物线y2=2px(p>0),一光源在点A(6,4)处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的B点,反射后,又射向抛物线上的C点,再反射后沿平行于抛物线的对称轴的方向射出,途中遇到直线l:x-y-7=0上的点D,再反射后又射回到A点,如图所示,则此抛物线的方程为( )
抛物线有光学性质,从焦点出发的光经抛物线反射后沿平行于抛物线的对称轴方向射出,今有抛物线y2=2px(p>0),一光源在点A(6,4)处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的B点,反射后,又射向抛物线上的C点,再反射后沿平行于抛物线的对称轴的方向射出,途中遇到直线l:x-y-7=0上的点D,再反射后又射回到A点,如图所示,则此抛物线的方程为( )| A、y2=2x |
| B、y2=4x |
| C、y2=8x |
| D、y2=16x |
考点:直线与圆锥曲线的关系
专题:圆锥曲线中的最值与范围问题
分析:首先,根据光线CD经直线l反射后又射向A点,得到直线CD与直线AD关于直线l对称.求解点A关于直线l的对称点为A′(11,-1),然后,得到点C的纵坐标,最后,确定p=2,从而得到其抛物线标准方程.
解答:
解:∵光线CD经直线l反射后又射向A点,
∴直线CD与直线AD关于直线l对称.
设点A关于直线l的对称点为A′(x′,y′),
∴
,
∴
,
∴
,
∴A′(11,-1),
∴直线CD的方程为y=-1,
∴点C的纵坐标为-1,
∵点A的纵坐标为4,
∴1×4=p2,
∴p=2,
∴抛物线的标准方程为:y2=4x,
故选:B.
∴直线CD与直线AD关于直线l对称.
设点A关于直线l的对称点为A′(x′,y′),
∴
|
∴
|
∴
|
∴A′(11,-1),
∴直线CD的方程为y=-1,
∴点C的纵坐标为-1,
∵点A的纵坐标为4,
∴1×4=p2,
∴p=2,
∴抛物线的标准方程为:y2=4x,
故选:B.
点评:本题重点考查了抛物线的标准方程、抛物线的几何性质、直线与抛物线的位置关系等知识,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
若圆x2+y2+mx-
=0与直线y=-1相切,且其圆心在y轴的左侧,则m的值为( )
| 1 |
| 4 |
| A、0 | ||
| B、2 | ||
| C、1 | ||
D、
|
数列{an}是等差数列的一个充要条件是(Sn是该数列前n项和)( )
| A、Sn=an+b |
| B、Sn=an2+bn+c |
| C、Sn=an2+bn (a≠0) |
| D、Sn=an2+bn |
双曲线
-
=1(a>0,b>0)的离心率是2,则渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、3x±y=0 | ||
B、x±
| ||
| C、x±3y=0 | ||
D、
|
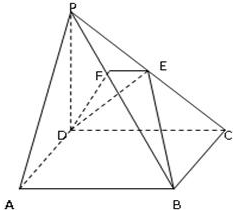 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ACD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ACD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.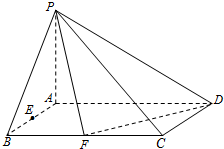 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.