题目内容
已知动点M(x,y)到直线l:x=-8的距离是它到点N(-2,0)的距离的2倍.
(1)求动点M的轨迹C的方程.
(2)是否存在直线m过点P(0,-6)与动点M的轨迹C交于A,B两点,且A是PB的中点?若不存在,请说明理由;若存在,求出直线m的斜率.
(1)求动点M的轨迹C的方程.
(2)是否存在直线m过点P(0,-6)与动点M的轨迹C交于A,B两点,且A是PB的中点?若不存在,请说明理由;若存在,求出直线m的斜率.
考点:轨迹方程,直线与圆锥曲线的关系
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)直接由题目给出的条件列式化简即可得到动点M的轨迹C的方程;
(2)经分析当直线m的斜率不存在时,不满足A是PB的中点,然后设出直线m的斜截式方程,和椭圆方程联立后整理,利用根与系数关系写出x1+x2,x1x2,结合2x1=x2得到关于k的方程,则直线m的斜率可求.
(2)经分析当直线m的斜率不存在时,不满足A是PB的中点,然后设出直线m的斜截式方程,和椭圆方程联立后整理,利用根与系数关系写出x1+x2,x1x2,结合2x1=x2得到关于k的方程,则直线m的斜率可求.
解答:
解:(Ⅰ1)点M(x,y)到直线x=-8的距离是它到点N(-2,0)的距离的2倍,则
|x+8|=2
,即(x+8)2=4[(x+2)2+y2],
整理得
+
=1.
所以,动点M的轨迹是椭圆,方程为
+
=1;
(2)P(0,-6),设A(x1,y1),B(x2,y2),由A是PB的中点,得2x1=0+x2,2y1=-6+y2.
由题意,直线m的斜率k存在.设直线m的方程为:y=kx-6.
代入椭圆方程,整理得:(3+4k2)x2-48kx+96=0.
所以x1+x2=
,x1x2=
.
因为2x1=x2.
则
+
=
,
所以
=
.
解得k=±
.
所以,直线m的斜率k=±
.
|x+8|=2
| (x+2)2+y2 |
整理得
| x2 |
| 16 |
| y2 |
| 12 |
所以,动点M的轨迹是椭圆,方程为
| x2 |
| 16 |
| y2 |
| 12 |
(2)P(0,-6),设A(x1,y1),B(x2,y2),由A是PB的中点,得2x1=0+x2,2y1=-6+y2.
由题意,直线m的斜率k存在.设直线m的方程为:y=kx-6.
代入椭圆方程,整理得:(3+4k2)x2-48kx+96=0.
所以x1+x2=
| 48k |
| 3+4k2 |
| 96 |
| 3+4k2 |
因为2x1=x2.
则
| x1 |
| x2 |
| x2 |
| x1 |
| 5 |
| 2 |
所以
(
| ||||
|
| 5 |
| 2 |
解得k=±
| 3 |
| 2 |
所以,直线m的斜率k=±
| 3 |
| 2 |
点评:本题考查了曲线方程,考查了直线与圆锥曲线的位置关系,考查了学生的计算能力,关键是看清题中给出的条件,灵活运用韦达定理,中点坐标公式进行求解,是中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
若集合A={0,1,2,3,4},集合B={x|x∈A且x-2∉A},则集合B的子集的个数为 ( )
| A、1 | B、2 | C、4 | D、8 |
设函数f(x)的定义域为M,若函数f(x)满足条件[m,n]⊆M,使f(x)在[m,n]上的值域是[
,
],则成f(x)为“半缩函数”,若函数f(x)=log3(3x+λ)为“半缩函数”,则λ的范围是( )
| m |
| 2 |
| n |
| 2 |
| A、(0,1) | ||
B、(0,
| ||
C、(0,
| ||
D、(
|
数列{an}是等差数列的一个充要条件是(Sn是该数列前n项和)( )
| A、Sn=an+b |
| B、Sn=an2+bn+c |
| C、Sn=an2+bn (a≠0) |
| D、Sn=an2+bn |
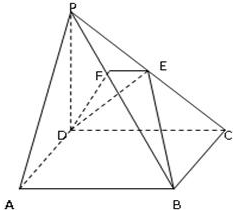 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ACD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ACD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.