题目内容
定义在R上的函数f(x)满足f(-x)=-f(x),f(x-2)=f(x+2),且x∈(-1,0)时,f(x)=2x+
,则f(log220)=( )
| 1 |
| 5 |
| A、-1 | ||
B、
| ||
| C、1 | ||
D、-
|
考点:函数的值
专题:函数的性质及应用
分析:由已知得函数f(x)为奇函数,函数f(x)为周期为4是周期函数,4<log220<5,f(log220)=-f(log2
),由f(log2
)=1,能求出f(log220)=-1.
| 4 |
| 5 |
| 4 |
| 5 |
解答:
解:∵定义在R上的函数f(x)满足f(-x)=-f(x),
∴函数f(x)为奇函数
又∵f(x-2)=f(x+2)
∴函数f(x)为周期为4是周期函数
又∵log232>log220>log216
∴4<log220<5
∴f(log220)=f(log220-4)=f(log2
)=-f(-log2
)=-f(log2
)
又∵x∈(-1,0)时,f(x)=2x+
,
∴f(log2
)=1
故f(log220)=-1.
故选:A.
∴函数f(x)为奇函数
又∵f(x-2)=f(x+2)
∴函数f(x)为周期为4是周期函数
又∵log232>log220>log216
∴4<log220<5
∴f(log220)=f(log220-4)=f(log2
| 5 |
| 4 |
| 5 |
| 4 |
| 4 |
| 5 |
又∵x∈(-1,0)时,f(x)=2x+
| 1 |
| 5 |
∴f(log2
| 4 |
| 5 |
故f(log220)=-1.
故选:A.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质和对数运算法则的合理运用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
数列{an}的通项公式an=
,若{an}的前n项和为24,则n为( )
| 1 | ||||
|
| A、25 | B、576 |
| C、624 | D、625 |
若圆x2+y2+mx-
=0与直线y=-1相切,且其圆心在y轴的左侧,则m的值为( )
| 1 |
| 4 |
| A、0 | ||
| B、2 | ||
| C、1 | ||
D、
|
数列{an}是等差数列的一个充要条件是(Sn是该数列前n项和)( )
| A、Sn=an+b |
| B、Sn=an2+bn+c |
| C、Sn=an2+bn (a≠0) |
| D、Sn=an2+bn |
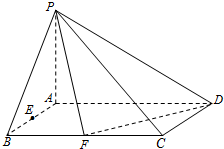 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.