题目内容
双曲线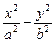 =1的实轴为A1A2,点P是双曲线上的一个动点,引A1Q⊥A1P,A2Q⊥A2P,A1Q与A2Q的交点为Q,求Q点的轨迹方程.
=1的实轴为A1A2,点P是双曲线上的一个动点,引A1Q⊥A1P,A2Q⊥A2P,A1Q与A2Q的交点为Q,求Q点的轨迹方程.
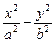 =1的实轴为A1A2,点P是双曲线上的一个动点,引A1Q⊥A1P,A2Q⊥A2P,A1Q与A2Q的交点为Q,求Q点的轨迹方程.
=1的实轴为A1A2,点P是双曲线上的一个动点,引A1Q⊥A1P,A2Q⊥A2P,A1Q与A2Q的交点为Q,求Q点的轨迹方程. Q点的轨迹方程为: a2x2-b2y2=a4(x≠±a)
设P(x0,y0)(x≠±a),Q(x,y).
∵A1(-a,0),A2(a,0).
由条件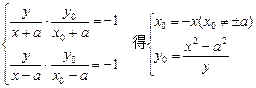
而点P(x0,y0)在双曲线上,∴b2x02-a2y02=a2b2
即b2(-x2)-a2(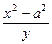 )2=a2b2
)2=a2b2
化简得Q点的轨迹方程为: a2x2-b2y2=a4(x≠±a).
∵A1(-a,0),A2(a,0).
由条件
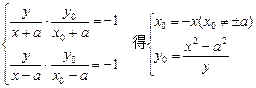
而点P(x0,y0)在双曲线上,∴b2x02-a2y02=a2b2

即b2(-x2)-a2(
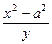 )2=a2b2
)2=a2b2化简得Q点的轨迹方程为: a2x2-b2y2=a4(x≠±a).

练习册系列答案
相关题目
 ,动点
,动点 满足条件:
满足条件: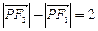 ,点
,点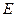 ,直线
,直线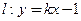 与曲线
与曲线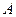 、
、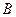 两点。如果
两点。如果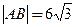 。(Ⅰ)求直线
。(Ⅰ)求直线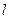 的方程;
的方程; ,使
,使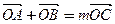 ,求
,求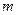 的值。
的值。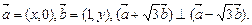
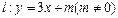 与曲线C交于A,B两点,D(0,-1)且有|AD|=|BD|,试求m的值.
与曲线C交于A,B两点,D(0,-1)且有|AD|=|BD|,试求m的值.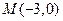 ,
,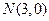 ,
,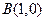 ,动圆
,动圆 与直线
与直线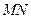 切于点
切于点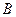 ,过
,过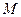 、
、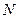 与圆
与圆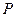 ,则
,则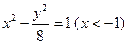

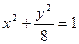 (x > 0)
(x > 0)
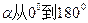 变化时,曲线
变化时,曲线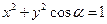 怎样变化?
怎样变化?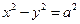 及其上一点
及其上一点 ,求证:(1)离心率
,求证:(1)离心率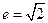 ,渐近线方程为
,渐近线方程为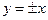 ;(2)
;(2)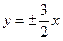 ,则离心率为
,则离心率为 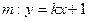 和双曲线
和双曲线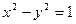 的左支交于不同两点,则
的左支交于不同两点,则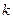 的取值范围是——————
的取值范围是——————