题目内容
【题目】过抛物线C:y2=2px(p>0)的焦点F的直线交抛物线于A,B两点,且A,B两点的纵坐标之积为﹣4.
(1)求抛物线C的方程;
(2)已知点D的坐标为(4,0),若过D和B两点的直线交抛物线C的准线于P点,求证:直线AP与x轴交于一定点.
【答案】
(1)解:设A(x1,y1),B(x2,y2),
设直线AB的方程为x=my+ ![]()
与抛物线的方程联立 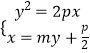 ,得y2﹣2mpy﹣p2=0,
,得y2﹣2mpy﹣p2=0,
∴y1y2=﹣p2=﹣4,
解得p=±2,
∵p>0,
∴p=2
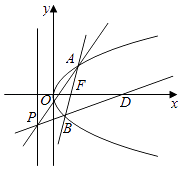
(2)解:依题意,直线BD与x轴不垂直,∴x2=4.
∴直线BD的方程可表示为,y= ![]() (x﹣4)①
(x﹣4)①
∵抛物线C的准线方程为,x=﹣1②
由①,②联立方程组可求得P的坐标为(﹣1,﹣ ![]() )
)
由(1)可得y1y2=﹣4,
∴P的坐标可化为(﹣1, ![]() ),
),
∴kAP= ![]() =
= ![]() ,
,
∴直线AP的方程为y﹣y1= ![]() (x﹣x1),
(x﹣x1),
令y=0,可得x=x1﹣ ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]()
∴直线AP与x轴交于定点( ![]() ,0).
,0).
【解析】(1)设A(x1 , y1),B(x2 , y2),设直线AB的方程为x=my+ ![]() ,联立方程组,根据A,B两点的纵坐标之积为﹣4,即可求出p的值,(2)表示出直线BD的方程可表示为,y=
,联立方程组,根据A,B两点的纵坐标之积为﹣4,即可求出p的值,(2)表示出直线BD的方程可表示为,y= ![]() (x﹣4)①,抛物线C的准线方程为,x=﹣1②,构成方程组,解得P的坐标,求出直线AP的斜率,得到直线AP的方程,求出交点坐标即可.
(x﹣4)①,抛物线C的准线方程为,x=﹣1②,构成方程组,解得P的坐标,求出直线AP的斜率,得到直线AP的方程,求出交点坐标即可.

练习册系列答案
相关题目