题目内容
【题目】如图,在三棱台ABC﹣A1B1C1中,D,E分别是AB,AC的中点,B1E⊥平面ABC,△AB1C是等边三角形,AB=2A1B1,AC=2BC,∠ACB=90°.
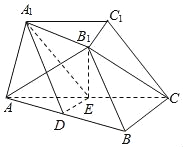
(1)证明:B1C∥平面A1DE;
(2)求二面角A﹣BB1﹣C的正弦值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(Ⅰ)先证明B1B∥平面A1DE,BC∥平面A1DE,再证平面B1BC∥平面A1DE,即证B1C∥平面A1DE. (Ⅱ)以ED,EC,EB1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系E﹣xyz,利用向量法求求二面角A﹣BB1﹣C的余弦值.
(Ⅰ)证明:因为A1B1∥AB,AB=2A1B1,D为棱AB的中点,所以A1B1∥BD,A1B1=BD,
所以四边形A1B1BD为平行四边形,从而BB1∥A1D.
又BB1平面A1DE,A1D平面A1DE,所以B1B∥平面A1DE,
因为DE是△ABC的中位线,所以DE∥BC,
同理可证,BC∥平面A1DE.
因为BB1∩BC=B,所以平面B1BC∥平面A1DE,
又B1C平面B1BC,所以B1C∥平面A1DE.
(Ⅱ)以ED,EC,EB1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系E﹣xyz,
设BC=a,则A(0,﹣a,0),B(a,a,0),C(0,a,0),![]() =(0,0,
=(0,0,![]() ),
),
则![]() =(0,a,
=(0,a,![]() ),
),![]() =(a,2a,0).
=(a,2a,0).
设平面ABB1的一个法向量![]() =(x1,y1,z1),
=(x1,y1,z1),
则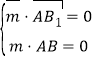 ,即
,即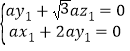 ,取z1=1,得
,取z1=1,得![]() =(
=(![]() ,
,![]() ,1).
,1).
同理,设平面BB1C的一个法向量![]() =(x,y,z),
=(x,y,z),
又![]() =(0,-a,
=(0,-a,![]() ),
),![]() =(-a,0,0),
=(-a,0,0),
由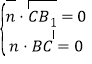 ,得
,得![]() ,取z=﹣1,得
,取z=﹣1,得![]() =(0,
=(0,![]() ,-1),
,-1),
以![]() =
=![]() =
=![]() ,
,
故二面角A﹣BB1﹣C的余弦值为:![]() .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目