Question

【题目】如图所示，三棱锥P﹣ABC中，D是AC的中点，，，．

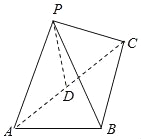
（1）求证：PD⊥平面ABC；

（2）求二面角P﹣AB﹣C的正切值大小．

Answer 1

【答案】(1)见解析 (2)

【解析】

（1）连接，推导出，由此能证明平面.（2）取的中点，连接，则,由，得，由平面，得，由，得平面，从而，进而是二面角的平面角，解三角形求得二面角的正切值．

（1）连接BD，∵D是AC的中点，，∴．

∵，，，∴．

∴，即AB⊥BC．

∴．

∵，，

∴．∴PD⊥BD．

∵AC∩BD=D，∴PD⊥平面ABC.

（2）取AB的中点E，连接DE、PE，

由E为AB的中点，知DE∥BC，

∵AB⊥BC，∴AB⊥DE．∵PD⊥平面ABC，∴PD⊥AB．

又AB⊥DE，，

∴AB⊥平面PDE，∴PE⊥AB．

∴是二面角P﹣AB﹣C的平面角．

在△PED中，，，，

∴ ．

∴二面角P﹣AB﹣C的正切值为．