题目内容
15．设X～N（-2，$\frac{1}{4}$），则X落在（-∞，-3.5]∪[-0.5，+∞）内的概率是（ ）| A． | 95.4% | B． | 99.7% | C． | 4.6% | D． | 0.3% |
分析 根据变量符合正态分布，看出均值和方差的值，根据3σ原则，知道区间（-3.5，-0.5）上的概率值，根据对称性和整个区间上的概率之和等于1，得到要求的结果．
解答 解：由题意μ=-2，σ=$\frac{1}{2}$，
∴P（-3.5＜X＜-0.5）=P（-2-3×0.5＜X＜-2+3×0.5）=0.9974，
∴P（X≤-3.5）+P（X≥-0.5）=1-P（-3.5＜X＜-0.5）=1-0.9974=0.0026．
故选D．
点评 本题考查正态分布曲线的特点及曲线所表示的意义，考查正态分布曲线的对称性和3σ原则，本题需要进行比较简单的运算，数字比较小，容易出错．
练习册系列答案
名校课堂系列答案
相关题目
10．在大街上，随机调查339名成人，有关吸烟、不吸烟、患支气管炎、不患支气管炎的数据如右表：根据表中数据，在犯错误的概率不超过0.01 的前提下判断吸烟与患支气管炎是否有关？
附：临界值表
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．
| 患慢性气管炎 | 未患慢性气管炎 | 总计 | |
| 吸烟 | 43 | 162 | 205 |
| 不吸烟 | 13 | 121 | 134 |
| 合计 | 56 | 283 | 339 |
| P（K2＞k0） | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
20．已知m，n是两条不重合的直线，α，β，γ是三个两两不重合的平面．给出下列四个命题：
①若m⊥α，m⊥β，则α∥β；
②若m?α，n?β，则α∥β；
③若α⊥γ，β⊥γ，则α∥β；
④若m、n是异面直线，m?α，m∥β，n?β，n∥α，则α∥β．
其中真命题是（ ）
①若m⊥α，m⊥β，则α∥β；
②若m?α，n?β，则α∥β；
③若α⊥γ，β⊥γ，则α∥β；
④若m、n是异面直线，m?α，m∥β，n?β，n∥α，则α∥β．
其中真命题是（ ）
| A． | ①和③ | B． | ①和② | C． | ①和④ | D． | ③和④ |
7．某赛事组委会要为获奖者定做某工艺品作为奖品，其中一等奖奖品3件，二等奖奖品6件．制作一等奖和二等奖奖品所用原料完全相同，但工艺不同，故价格有所差异．现有甲、乙两家工厂可以制作奖品（一等奖、二等奖奖品均符合要求），甲厂收费便宜，但原料有限，最多只能制作4件奖品，乙厂原料充足，但收费交贵，其具体收费情况如表：
求组委会定做该工艺品至少需要花费多少元钱．
| 奖品 收费（元/件） 工厂 | 一等奖奖品 | 二等奖奖品 |
| 甲 | 500 | 400 |
| 乙 | 800 | 600 |
4．
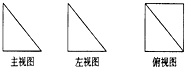如图，是一个空间几何体的主视图（正视图）、左视图、俯视图，如果图中直角三角形的直角边长均为1，那么这个几何体的侧面积为（ ）
如图，是一个空间几何体的主视图（正视图）、左视图、俯视图，如果图中直角三角形的直角边长均为1，那么这个几何体的侧面积为（ ）| A． | 1+$\sqrt{2}$ | B． | 2+$\sqrt{2}$ | C． | 1+2$\sqrt{2}$ | D． | 2+2$\sqrt{2}$ |
5．集合A={x|x2-2x≤0}，B={x|y=lg（1-x）}，则A∩（∁RB）等于（ ）
| A． | {x|0＜x≤1} | B． | {x|0≤x＜1} | C． | {x|1＜x≤2} | D． | {x|1≤x≤2} |