题目内容
17.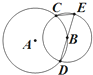 如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径,已知CE=1,DE=4,则圆A的半径为4.
如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径,已知CE=1,DE=4,则圆A的半径为4.
分析 连接CD,AB,交于O,则AB⊥CD,CE⊥CD,求出OB=$\frac{1}{2}$,CD=$\sqrt{15}$,设圆A的半径为r,则r2=($\frac{\sqrt{15}}{2}$)2+(r-$\frac{1}{2}$)2,即可求出圆A的半径.
解答 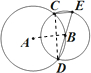 解:连接CD,AB,交于O,则AB⊥CD,CE⊥CD,
解:连接CD,AB,交于O,则AB⊥CD,CE⊥CD,
∴OB∥CE,OB=$\frac{1}{2}$CE,
∵CE=1,DE=4,DE为圆B的直径,
∴OB=$\frac{1}{2}$,CD=$\sqrt{15}$,
设圆A的半径为r,则r2=($\frac{\sqrt{15}}{2}$)2+(r-$\frac{1}{2}$)2,
∴r=4.
故答案为:4.
点评 本题考查垂径定理,考查圆的直径的性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
9.若$\frac{1}{27}$≤x≤9,则f(x)=log3$\frac{x}{27}$•log3(3x)( )
| A. | 有最小值-$\frac{32}{9}$,最大值-3 | B. | 有最小-4,最大值12 | ||
| C. | 有最小值-$\frac{32}{9}$,无最大值 | D. | 无最小值,有最大值12 |
6.已知向量$\overrightarrow a=(cosθ,sinθ)$,向量$\overrightarrow b=(\sqrt{3},-1)$,则|2$\overrightarrow a-\overrightarrow b|$的最大值,最小值分别是( )
| A. | 4,0 | B. | $4\sqrt{2}$,4 | C. | $4\sqrt{2}$,0 | D. | 16,0 |
7.函数f(x)=x•2|x|-x-2的零点个数为( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |