题目内容
5.函数y=$\frac{3+x+{x}^{2}}{1+x}$(x>0)的最小值是2$\sqrt{3}$-1.分析 利用凑配法和换元法,将函数的解析式化为对勾函数的形式,结合对勾函数的图象和性质,得到答案.
解答 解:函数y=$\frac{3+x+{x}^{2}}{1+x}$=$\frac{(x+1)^{2}-(x+1)+3}{x+1}$=x+1+$\frac{3}{x+1}$-1,
令t=x+1,t>1,
则y=t+$\frac{3}{t}$-1,
由y=t+$\frac{3}{t}$-1在(1,$\sqrt{3}$]上为减函数,在[$\sqrt{3}$,+∞)上为增函数,
故当t=$\sqrt{3}$时,函数取最小值2$\sqrt{3}$-1,
故答案为:2$\sqrt{3}$-1
点评 本题考查的知识点是函数的最值及其几何意义,其中利用凑配法和换元法,将函数的解析式化为对勾函数的形式,是解答的关键.

练习册系列答案
相关题目
15.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点分别为F1、F2,过F1作圆x2+y2=a2的切线分别交双曲线的左、右两支于点B、C,且|BC|=|CF2|,则双曲线的渐近线方程为( )
| A. | y=±3x | B. | y=±2$\sqrt{2}$x | C. | y=±($\sqrt{3}$+1)x | D. | y=±($\sqrt{3}$-1)x |
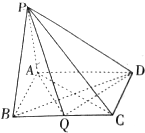 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).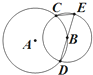 如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径,已知CE=1,DE=4,则圆A的半径为4.
如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径,已知CE=1,DE=4,则圆A的半径为4.