题目内容
12.下列命题正确的个数是( )A.“在三角形ABC中,若sinA>sinB,则A>B”的逆命题是真命题;
B.命题p:x≠2或y≠3,命题q:x+y≠5则p是q的必要不充分条件;
C.“?x∈R,x3-x2+1≤0”的否定是“?x∈R,x3-x2+1>0”;
D.“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 A项根据正弦定理以及四种命题之间的关系即可判断;
B项根据必要不充分条件的概念即可判断该命题是否正确;
C项根据全称命题和存在性命题的否定的判断;
D项写出一个命题的否命题的关键是正确找出原命题的条件和结论.
解答 解:对于A项“在△ABC中,若sinA>sinB,则A>B”的逆命题为“在△ABC中,若A>B,则sinA>sinB”,
若A>B,则a>b,根据正弦定理可知sinA>sinB,∴逆命题是真命题,∴A正确;
对于B项,由x≠2,或y≠3,得不到x+y≠5,比如x=1,y=4,x+y=5,∴p不是q的充分条件;
若x+y≠5,则一定有x≠2且y≠3,即能得到x≠2,或y≠3,∴p是q的必要条件;
∴p是q的必要不充分条件,所以B正确;
对于C项,“?x∈R,x3-x2+1≤0”的否定是“?x∈R,x3-x2+1>0”;所以C不对.
对于D项,“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”.所以D正确.
故选:C.
点评 本题主要考查各种命题的真假判断,涉及的知识点较多,综合性较强.

练习册系列答案
相关题目
1.复数$\frac{3+i}{1-3i}$+$\frac{1}{i}$等于( )
| A. | 3-i | B. | -2i | C. | 2i | D. | 0 |
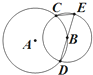 如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径,已知CE=1,DE=4,则圆A的半径为4.
如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径,已知CE=1,DE=4,则圆A的半径为4.